
| A. | p假q真 | B. | p假q假 | C. | p真q真 | D. | p真q假 |
分析 画出函数f(x)=的图象,根据a,b,c,d互不相等,且f(a)=f(b)=f(c)=f(d),令a<b<c<d,根据对数的运算性质,及c,d的取值范围得到abcd的取值范围,再利用对勾函数的单调性求出a+b+c+d的范围得答案.
解答 解:作出函数f(x)=$\left\{\begin{array}{l}{-|lnx|,x>0}\\{{x}^{2}+2x-1,x≤0}\end{array}\right.$的图象如图,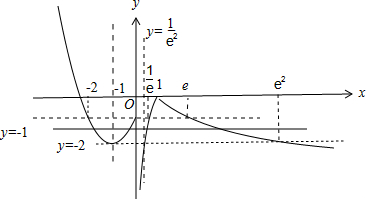
不妨设a<b<c<d,图中实线y=m与函数f(x)的图象相交于四个不同的点,由图可知m∈(-2,-1],
则a,b是x2+2x-m-1=0的两根,∴a+b=-2,ab=-m-1,
∴ab∈[0,1),且lnc=m,lnd=-m,
∴ln(cd)=0,
∴cd=1,
∴abcd∈[0,1),故①正确;
由图可知,c∈($\frac{1}{{e}^{2}},\frac{1}{e}$],
又∵cd=1,a+b=-2,
∴a+b+c+d=c+$\frac{1}{c}$-2,在($\frac{1}{{e}^{2}}$,$\frac{1}{e}$]是递减函数,
∴a+b+c+d∈[e+$\frac{1}{e}$-2,e2+$\frac{1}{{e}^{2}}$-2),故②正确.
∴p真q真.
故选:C.
点评 本题考查命题的真假判断与应用,考查对数函数图象与性质的综合应用,其中画出函数图象,利用图象的直观性,数形结合进行解答是解决此类问题的关键,是中档题.


 每课必练系列答案
每课必练系列答案科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=1,g(x)=x0 | B. | f(x)=x2,g(x)=(x+1)2 | ||
| C. | f(x)=x,g(x)=elnx | D. | f(x)=|x|,g(x)=$\left\{\begin{array}{l}{x,}&{x≥0}\\{-x,}&{x<0}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
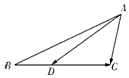 如图,在△ABC中,∠BAC=60°,AB=2,AC=1,D是BC边上一点,且$\overrightarrow{CD}$=2$\overrightarrow{DB}$,则$\overrightarrow{AD}$•$\overrightarrow{BC}$ 的值为-2.
如图,在△ABC中,∠BAC=60°,AB=2,AC=1,D是BC边上一点,且$\overrightarrow{CD}$=2$\overrightarrow{DB}$,则$\overrightarrow{AD}$•$\overrightarrow{BC}$ 的值为-2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com