
分析 (1)由题意可知及椭圆的定义:|F1E|+|MF2|=2a,|MF1|+|MF2|=2a,即可求得a的值,利用椭圆的离心率公式即可求得b和c的值,即可求得椭圆方程;
(2)设l方程为,代入椭圆方程,由题意可知($\overrightarrow{NP}$+$\overrightarrow{NQ}$)•$\overrightarrow{PQ}$=0,利用韦达定理即可求得$\overrightarrow{NP}$+$\overrightarrow{NQ}$,$\overrightarrow{PQ}$的方向向量为(1,k),根据向量数量积的坐标运算,即可求得k,求得直线l的方程.
解答 解:(1)设圆C与F1A的延长线切于点E,与线段AF2切于点D,
则|AD|=|AE|,|F2D|=|F2M|,|F1E|=|F1M|,
∵|AF1|+|AF2|=2a,∴|AF1|+|AD|+|DF2|=2a,
∴|F1E|+|MF2|=2a,|MF1|+|MF2|=2a,
∴(2-c)+(2+c)=2a,故a=2,由$c=\frac{{\sqrt{3}}}{2}$,可知$c=\sqrt{3},b=1$,
椭圆方程为$\frac{x^2}{4}+{y^2}=1$;
(2)由(1)可知F2($\sqrt{3}$,0),设l方程为$y=k({x-\sqrt{3}}),k≠0$,
代入椭圆方程可得$\left\{\begin{array}{l}{y=k(x-\sqrt{3})}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,
整理得:$({1+4{k^2}}){x^2}-8\sqrt{3}{k^2}x+12{k^2}-4=0$,
设P(x1,y1),Q(x2,y2),
则${x_1}+{x_2}=\frac{{8\sqrt{3}{k^2}}}{{1+4{k^2}}},{y_1}+{y_2}=k({{x_1}+{x_2}-2\sqrt{3}})=\frac{{-2\sqrt{3}k}}{{1+4{k^2}}}$,
以NP,NQ为邻边的平行四边形是菱形,
∴($\overrightarrow{NP}$+$\overrightarrow{NQ}$)•$\overrightarrow{PQ}$=0,$\overrightarrow{NP}$+$\overrightarrow{NQ}$=(x1-$\frac{\sqrt{3}}{2}$,y1)+(x2-$\frac{\sqrt{3}}{2}$,y2)
=$({{x_1}+{x_2}-\sqrt{3},{y_1}+{y_2}})=({\frac{{8\sqrt{3}{k^2}}}{{1+4{k^2}}}-\sqrt{3},\frac{{-2\sqrt{3}k}}{{1+4{k^2}}}})$,
$\overrightarrow{PQ}$的方向向量为(1,k),
∴$\frac{8\sqrt{3}{k}^{2}}{1+4{k}^{2}}$-$\sqrt{3}$-$\frac{2\sqrt{3}{k}^{2}}{1+4{k}^{2}}$=0,$k=±\frac{{\sqrt{2}}}{2}$,
∴直线l的方程$y=±\frac{{\sqrt{2}}}{2}({x-\sqrt{3}})$.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理,向量的坐标运算,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $a≤-\frac{1}{4}$ | B. | a≤0 | C. | $a≤\frac{1}{4}$ | D. | a≤2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
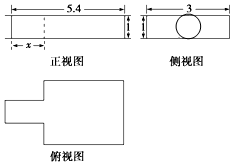 中国古代数学著作《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,一个爱好者根据该标准量器制作了一个几何体模型,该几何体的三视图如图所示(单位:寸),若几何体体积为13.5(立方寸),(π取3),则图中x的为( )
中国古代数学著作《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,一个爱好者根据该标准量器制作了一个几何体模型,该几何体的三视图如图所示(单位:寸),若几何体体积为13.5(立方寸),(π取3),则图中x的为( )| A. | 2.4 | B. | 1.8 | C. | 1.6 | D. | 1.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p假q真 | B. | p假q假 | C. | p真q真 | D. | p真q假 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{16}$ | B. | $\frac{5}{8}$ | C. | $\frac{9}{16}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com