
分析 由题意,只要求出f(x)=x3-2x2-4x在[-1,3]最值,使$\frac{2m}{27}$-2大于|f(x1)-f(x2)|max,然后求m 的范围.
解答 解:f'(x)=3x2-4x-4=(x-2)(3x+2),所以f(x)在(-1,$-\frac{2}{3}$)递增,在($-\frac{2}{3}$,2)递减,(2,3)递增,
并且f(-1)=1,f(-$\frac{2}{3}$)=$\frac{40}{27}$,f(2)=-8,f(3)=-3,
所以f(x)=x3-2x2-4x在[-1,3]最大值是$\frac{40}{27}$,最小值是-8,
所以|f(x1)-f(x2)|max=$\frac{256}{27}$,所以只要$\frac{2m}{27}$-2>$\frac{256}{27}$,解得m>155;
所以m>155.
点评 本题考查了函数的单调性和最值的关系以及恒成立问题,属于中档题.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{3}$,$\frac{2}{3}$,-$\frac{2}{3}$) | B. | ($\frac{1}{3}$,-$\frac{2}{3}$,$\frac{2}{3}$) | C. | (-$\frac{1}{3}$,$\frac{2}{3}$,-$\frac{2}{3}$) | D. | ±($\frac{1}{3}$,-$\frac{2}{3}$,$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
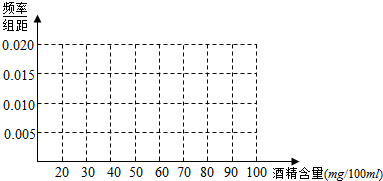
| 酒精含量(mg/100ml) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 人数 | 3 | 4 | 1 | 4 | 2 | 3 | 2 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com