
(1)求平面PCD与平面ABCD所成二面角的大小;
(2)求证:平面MND⊥平面PCD;
(3)当AB的长度变化时,求异面直线PC与AD所成角的取值范围.
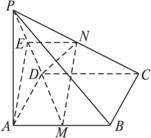
(1)解:PA⊥平面ABCD,CD⊥AD,
∴PD⊥CD,故∠PDA是平面PCD与平面ABCD所成二面角的平面角.在Rt△PAD中,PA⊥AD,PA=AD,
∴∠PDA=45°.
(2)证明:如图所示,取PD中点E,连结AE、EN,由M、N分别是AB、PC的中点,

∴EN![]()
![]() CD
CD![]()
![]() AB.
AB.
∴AMNE是平行四边形,
∴MN∥AE.
在等腰Rt△PAD中,AE是斜边的中线,
∴AE⊥PD.
又CD⊥PD,
∴CD⊥平面PAD.
∴CD⊥AE.
又PD∩CD={a},
∴AE⊥平面PCD.
∴MN⊥平面PCD.
∴平面MND⊥平面PCD.
(3)解:∵AD∥BC,
∴∠PCB为异面直线PC、AD所成的角.
由三垂线定理知PB⊥BC,设AB=x(x>0),
∴tan∠PCB=![]() =
=![]() >1.又∠PCB为锐角,
>1.又∠PCB为锐角,
∴∠PCB∈(![]() ,
,![]() ),即异面直线PC、AD所成的角的范围为(
),即异面直线PC、AD所成的角的范围为(![]() ,
,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2010-2011学年重庆市高三下学期第一次月考考试数学理卷 题型:解答题
(本小题满分13分)
如图PA⊥平面ABCD,四边形ABCD是矩形,E、F分别是AB,PD的中点.
(1)求证:AF//平面PCE;
(2)若PA=AD且AD=2,CD=3,求P—CE—A的正切值.

查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求平面PCD与平面ABCD所成二面角的大小;
(2)求证:平面MND⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求平面PCD与平面ABCD所成二面角的大小;
(2)求证:平面MND⊥平面PCD;
(3)当AB的长度变化时,求异面直线PC与AD所成角的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com