
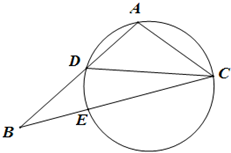
 如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=2,AB=3,EC=
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=2,AB=3,EC=| 5 |
| 2 |
| 3 |
| 2 |
| BE |
| BA |
| DE |
| CA |

| 5 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 3 |


科目:高中数学 来源: 题型:
| 3 |
| 3 |
|
| 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
| a |
| x0+2 |
| b |
| x0+1 |
| 1-2a |
| x0 |
| x0 |
| x0+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
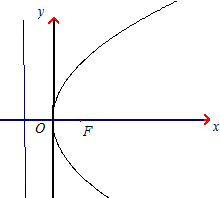 已知抛物线y2=2px(p>0),其焦点为F,一条过焦点F,倾斜角为θ(0<θ<π)的直线交抛物线于A,B两点,连接AO(O为坐标原点),交准线于点B',连接BO,交准线于点A',求四边形ABB'A'的面积.
已知抛物线y2=2px(p>0),其焦点为F,一条过焦点F,倾斜角为θ(0<θ<π)的直线交抛物线于A,B两点,连接AO(O为坐标原点),交准线于点B',连接BO,交准线于点A',求四边形ABB'A'的面积.查看答案和解析>>
科目:高中数学 来源: 题型:
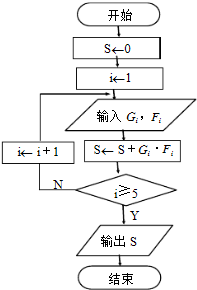 为了了解广东人的生活幸福指数,对40到60岁中年人一天的运动时间(单位:t),现随机地选出50名做调查,下表是一天运动时间频率分布表:
为了了解广东人的生活幸福指数,对40到60岁中年人一天的运动时间(单位:t),现随机地选出50名做调查,下表是一天运动时间频率分布表:| 序号(i) | 分组 | 组中值(Gi) | 频数 | 频率(Fi) |
| 1 | [0,1) | 0.5 | 6 | 0.12 |
| 2 | [1,2) | 1.5 | 10 | 0.2 |
| 3 | [2,3) | 2.5 | 20 | 0.4 |
| 4 | [3,4) | 3.5 | 10 | 0.2 |
| 5 | [4,5] | 4.5 | 4 | 0.08 |
查看答案和解析>>
科目:高中数学 来源: 题型:
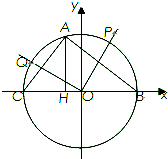 如图,已知B、C是以原点O为圆心,半径为1的圆与x轴的交点,点A在劣弧
如图,已知B、C是以原点O为圆心,半径为1的圆与x轴的交点,点A在劣弧 |
| PQ |
| AH |
| AB |
| AC |
A、(0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com