练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    四棱锥P－ABCD的五个顶点都在一个球面上，该四棱锥的三视图如图所示，E，F分别是棱AB，CD的中点，直线EF被球面截得的线段长为2，则该球的表面积为(　　)

    A．9π                                                           B．3π

    C．2π                                                     D．12π


    D

    [解析]　该几何体的直观图如图所示，

    该几何体可看作由正方体截得的，则正方体外接球的直径即为PC.由直线EF被球面所截得的线段长为2，可知正方形ABCD的对角线AC的长为2，可得a＝2，在△PAC中，PC＝＝2，

    ∴球的半径R＝，∴S表＝4πR2＝4π×()2＝12π.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设曲线x2－y2＝0与抛物线y2＝－4x的准线围成的三角形区域(包含边界)为D，P(x，y)为D内的一个动点，则目标函数z＝x－2y＋5的最大值为(　　)

    A．4　　　　                                                 B．5　　　　

    C．8　　　　                                                 D．12

    查看答案和解析>>

    科目：高中数学 来源： 题型：


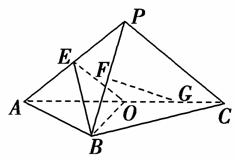
    如图，平面PAC⊥平面ABC，△ABC是以AC为斜边的等腰直角三角形，E，F，O分别为PA，PB，AC的中点，AC＝16，PA＝PC＝10.

    (1)设G是OC的中点，证明：FG∥平面BOE；

    (2)证明在△ABO内存在一点M，使FM⊥平面BOE，并求点M到OA，OB的距离．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在四棱锥P－ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，AB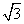＝，BC＝1，PA＝2，E为PD的中点．

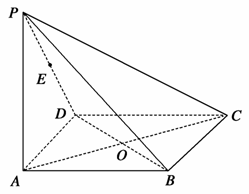
    (1)求直线AC与PB所成角的余弦值；

    (2)在侧面PAB内找一点N，使NE⊥平面PAC，并求出点N到AB和AP的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知某几何体的俯视图是如图所示的边长为2的正方形，正视图与侧视图是边长为2的正三角形，则其表面积是(　　)

    A．8                                                             B．12

    C．4(1＋)                                               D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    侧棱长为2的正三棱锥V－ABC中，∠AVB＝∠BVC＝∠CVA＝40°，过点A作截面AEF，则截面△AEF周长的最小值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


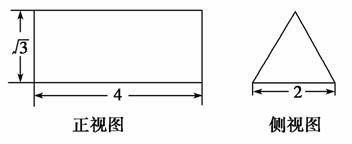
    已知正三棱柱ABC－A′B′C′的正视图和侧视图如图所示．设△ABC，△A′B′C′的中心分别是O，O′，现将此三棱柱绕直线OO′旋转，在旋转过程中对应的俯视图的面积为S，则S的最大值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设l为直线，α，β是两个不同的平面．下列命题中正确的是(　　)

    A．若l∥α，l∥β，则α∥β

    B．若l⊥α，l⊥β，则α∥β

    C．若l⊥α，l∥β，则α∥β

    D．若α⊥β，l∥α，则l⊥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设两个平面α、β，直线l，下列三个条件：①l⊥α；②l∥β；③α⊥β.若以其中两个作为前提，另一个作为结论，则可构成三个命题，这三个命题中正确命题的个数为(　　)

    A．3　　 　　                                               B．2　　 　　

    C．1　　 　　                                               D．0

    查看答案和解析>>

    同步练习册答案