
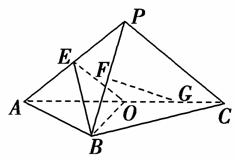
如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,AC=16,PA=PC=10.
(1)设G是OC的中点,证明:FG∥平面BOE;
(2)证明在△ABO内存在一点M,使FM⊥平面BOE,并求点M到OA,OB的距离.
(1)
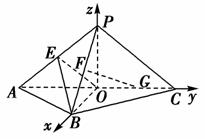
证明:如图,连接OP,以点O为坐标原点,分别以OB、OC、OP所在直线为x轴、y轴、z轴,建立空间直角坐标系O-xyz,由条件知,OA=OC=8,PO=6,OB=8,则O(0,0,0),A(0,-8,0),B(8,0,0),C(0,8,0),P(0,0,6),E(0,-4,3),F(4,0,3),G(0,4,0).
因为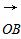 =(8,0,0),
=(8,0,0),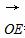 =(0,-4,3),
=(0,-4,3),
所以平面BOE的法向量n=(0,3,4),
由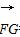 =(-4,4,-3),得n·
=(-4,4,-3),得n·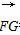 =0.
=0.
又直线FG不在平面BOE内,
所以FG∥平面BOE.
(2)设点M的坐标为(x0,y0,0),
则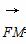 =(x0-4,y0,-3).
=(x0-4,y0,-3).
要使FM⊥平面BOE,只需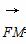 ∥n,
∥n,
因此x0=4,y0=-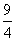 ,
,
即点M的坐标是(4,-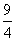 ,0).
,0).
在平面直角坐标系xOy中,△AOB的内部区域可表示为不等式组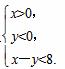
经检验,点M的坐标满足上述不等式组,所以在△AOB内存在一点M,使FM⊥平面BOE.
由点M的坐标得点M到OA,OB的距离分别为4,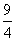 .
.


科目:高中数学 来源: 题型:
在直角坐标系xOy中,点M(2,-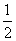 ),点F在抛物线C:y=mx2(m>0)的焦点,线段MF恰被抛物线C平分.
),点F在抛物线C:y=mx2(m>0)的焦点,线段MF恰被抛物线C平分.
(1)求m的值;
(2)过点M作直线l交抛物线C于A、B两点,设直线FA、FM、FB的斜率分别为k1、k2、k3,问k1、k2、k3能否成公差不为零的等差数列?若能,求直线l的方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在正方体ABCD-A1B1C1D1中,M、N分别是棱CD、CC1的中点,则异面直线A1M与DN所成的角的大小是( )
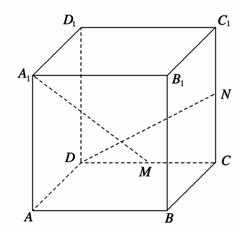
A.30° B.45°
C.60° D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
四棱锥P-ABCD的五个顶点都在一个球面上,该四棱锥的三视图如图所示,E,F分别是棱AB,CD的中点,直线EF被球面截得的线段长为2 ,则该球的表面积为( )
,则该球的表面积为( )

A.9π B.3π
C.2 π D.12π
π D.12π
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.

求证:(1)平面EFG∥平面ABC;
(2)BC⊥SA.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com