
如图,在正方体ABCD-A1B1C1D1中,M、N分别是棱CD、CC1的中点,则异面直线A1M与DN所成的角的大小是( )
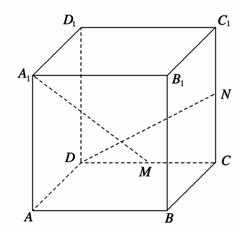
A.30° B.45°
C.60° D.90°
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB.已知AB=4,AC=6,BD=8,CD=2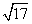 ,则该二面角的大小为( )
,则该二面角的大小为( )
A.150° B.45°
C.60° D.120°
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,AC=16,PA=PC=10.
(1)设G是OC的中点,证明:FG∥平面BOE;
(2)证明在△ABO内存在一点M,使FM⊥平面BOE,并求点M到OA,OB的距离.
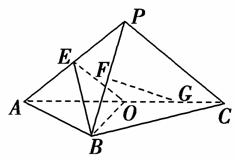
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=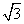 ,BC=1,PA=2,E为PD的中点.
,BC=1,PA=2,E为PD的中点.
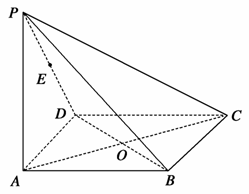
(1)求直线AC与PB所成角的余弦值;
(2)在侧面PAB内找一点N,使NE⊥平面PAC,并求出点N到AB和AP的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
若空间中有四个点,则“这四个点中有三点在同一条直线上”是“这四个点在同一个平面上”的( )
A.充分非必要条件 B.必要非充分条件
C.充分必要条件 D.既非充分又非必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com