
分析 先求出函数的导数,得到函数的单调区间,从而求出函数的最大值.
解答 解:y′=$\frac{1}{2}$-sinx,x∈[-$\frac{π}{2}$,$\frac{π}{2}$],
令y′>0,解得:-$\frac{π}{2}$≤x<$\frac{π}{6}$,
令y′<0,解得:$\frac{π}{6}$<x≤$\frac{π}{2}$,
∴函数y=$\frac{1}{2}$x+cosx在[-$\frac{π}{2}$,$\frac{π}{6}$)递增,在($\frac{π}{6}$,$\frac{π}{2}$]递减,
∴y最大值=y极大值=${y|}_{x=\frac{π}{6}}$=$\frac{π}{12}$+$\frac{\sqrt{3}}{2}$,
故答案为:$\frac{π}{12}$+$\frac{\sqrt{3}}{2}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道基础题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 若m∥β,β⊥α则m⊥α | B. | 若m⊥n,n⊥β,β⊥α,则m⊥α | ||
| C. | 若m⊥α,m⊥n则n∥α | D. | 若m⊥α,n?α,则m⊥n |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
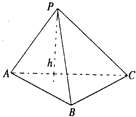 在Rt△ABC中,两直角边分别为a,b,设h为斜边上的高,则$\frac{1}{h^2}$=$\frac{1}{a^2}$+$\frac{1}{b^2}$,类比此性质,如图,在四面体P-ABC 中,若PA,PB,PC两两垂直,且长度分别为a,b,c,设棱锥底面ABC上的高为h,则得到的正确结论为$\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$.
在Rt△ABC中,两直角边分别为a,b,设h为斜边上的高,则$\frac{1}{h^2}$=$\frac{1}{a^2}$+$\frac{1}{b^2}$,类比此性质,如图,在四面体P-ABC 中,若PA,PB,PC两两垂直,且长度分别为a,b,c,设棱锥底面ABC上的高为h,则得到的正确结论为$\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-2,\frac{3}{2})$ | B. | $(-2,\frac{3}{2}]$ | C. | [-3,2] | D. | (-3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$n(n+1)(n+2) | B. | $\frac{1}{3}$n(n+1)(n+3) | C. | $\frac{1}{3}$n(n+1)(n+4) | D. | $\frac{1}{3}$n(n+1)(n+5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com