
【题目】已知点![]() ,点
,点![]() ,点
,点![]() ,动圆
,动圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 相切于点
相切于点![]() (
(![]() 均不同于点
均不同于点![]() ),且
),且![]() 与
与![]() 交于点
交于点![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)证明:![]() 为定值,并求
为定值,并求![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() 两点,当
两点,当![]() 三点共线时,求四边形
三点共线时,求四边形![]() 的面积.
的面积.
【答案】(1)证明见解析,方程为![]() .
.
(2) ![]() .
.
【解析】分析:(1)根据圆的切线性质可得,![]()
![]() ,从而根据椭圆的可得结果;(2)直线与曲线联立,利用韦达定理、弦长公式以及三角形面积公式可得四边形
,从而根据椭圆的可得结果;(2)直线与曲线联立,利用韦达定理、弦长公式以及三角形面积公式可得四边形![]() 的面积为
的面积为![]() .
.
详解:(1)由已知可得|PD|=|PE|,|BA|=|BD|,|CE|=|CA|,
所以|PB|+|PC|=|PD|+|DB|+|PC|
=|PE|+|PC|+|AB|
=|CE|+|AB|
=|AC|+|AB|=4>|BC|
所以点P的轨迹是以B,C为焦点的椭圆(去掉与x轴的交点),
可求的方程为![]() +
+![]() =1(y≠0).
=1(y≠0).
(2)由O,D,C三点共线及圆的几何性质,可知PB⊥CD,
又由直线CE,CA为圆O的切线,可知CE=CA,OA=OE,
所以△OAC≌△OEC,进而有∠ACO=∠ECO,
所以|PC|=|BC|=2,又由椭圆的定义,|PB|+|PC|=4,得|PB|=2,
所以△PBC为等边三角形,即点P在y轴上,点P的坐标为(0,±![]() )
)
(i)当点P的坐标为(0,![]() )时,∠PBC=60,∠BCD=30,
)时,∠PBC=60,∠BCD=30,
此时直线l1的方程为y=![]() (x+1),直线CD的方程为y=-
(x+1),直线CD的方程为y=-![]() (x-1),
(x-1),
由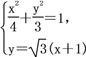 整理得5x2+8x=0,得Q(-
整理得5x2+8x=0,得Q(-![]() ,-
,-![]() ),所以|PQ|=
),所以|PQ|=![]() ,
,
由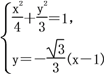 整理得13x2-8x-32=0,
整理得13x2-8x-32=0,
设M(x1,y1),N(x2,y2),x1+x2=![]() ,x1x2=-
,x1x2=-![]() ,
,
|MN|=![]() |x1-x2|=
|x1-x2|=![]() ,
,
所以四边形MPNQ的面积S=![]() |PQ|·|MN|=
|PQ|·|MN|=![]() .
.
(ii)当点P的坐标为(0,-![]() )时,由椭圆的对称性,四边形MPNQ的面积为
)时,由椭圆的对称性,四边形MPNQ的面积为![]() .
.
综上,四边形MPNQ的面积为![]() .
.


科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 甲、乙二人比赛,甲胜的概率为![]() ,则比赛5场,甲胜3场
,则比赛5场,甲胜3场
B. 某医院治疗一种疾病的治愈率为10%,前9个病人没有治愈,则第10个病人一定治愈
C. 随机试验的频率与概率相等
D. 天气预报中,预报明天降水概率为90%,是指降水的可能性是90%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆方程;
(2)斜率为![]() 的直线
的直线![]() 过点F,且与椭圆交于
过点F,且与椭圆交于![]() 两点,P为直线
两点,P为直线![]() 上的一点,
上的一点,
若![]() 为等边三角形,求直线
为等边三角形,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左焦点
的左焦点![]() ,离心率为
,离心率为![]() ,点
,点![]() 为椭圆
为椭圆![]() 上任一点,且
上任一点,且![]() 的最小值为
的最小值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 过椭圆的左焦点
过椭圆的左焦点![]() ,与椭圆交于
,与椭圆交于![]() 两点,且
两点,且![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.
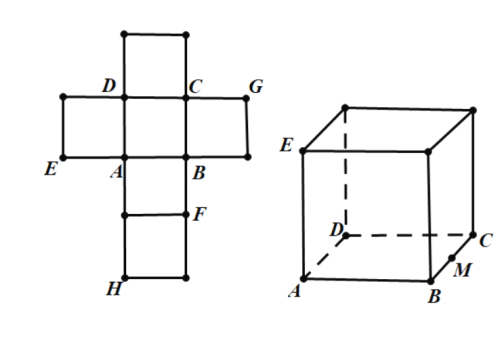
(Ⅰ)请按字母F,G,H标记在正方体相应地顶点处(不需要说明理由)
(Ⅱ)判断平面BEG与平面ACH的位置关系.并说明你的结论.
(Ⅲ)证明:直线DF![]() 平面BEG
平面BEG
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四种说法正确的是( )
①若![]() 和
和![]() 都是定义在
都是定义在![]() 上的函数,则“
上的函数,则“![]() 与
与![]() 同是奇函数”是“
同是奇函数”是“![]() 是偶函数”的充要条件
是偶函数”的充要条件
②命题 “![]() ”的否定是“
”的否定是“![]()
![]() ≤0”
≤0”
③命题“若x=2,则![]() ”的逆命题是“若
”的逆命题是“若![]() ,则x=2”
,则x=2”
④命题![]() :在
:在![]() 中,若
中,若![]() ,则
,则![]() ;
;
命题![]() :
:![]() 在第一象限是增函数;
在第一象限是增函数;
则![]() 为真命题
为真命题
A. ①②③④ B. ①③ C. ③④ D. ③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com