
| A. | 3 | B. | 6 | C. | 9 | D. | 18 |
分析 设对角线AC、BD相交于O点,根据平行四边形的性质与向量加法法则,得到$\overrightarrow{AC}$=2$\overrightarrow{AO}$=2($\overrightarrow{AP}$+$\overrightarrow{PO}$),从而可得$\overrightarrow{AP}•\overrightarrow{AC}$=2$\overrightarrow{AP}•\overrightarrow{AO}$=2${\overrightarrow{AP}}^{2}$+2$\overrightarrow{AP}$•$\overrightarrow{PO}$.再由$\overrightarrow{AP}$2=$\overrightarrow{|AP|}$2=9且$\overrightarrow{AP}$•$\overrightarrow{PO}$=0,代入前面的式子即可得到$\overrightarrow{AP}•\overrightarrow{AC}$的值.
解答 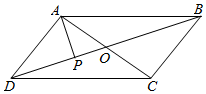 解:设对角线AC、BD相交于O点,
解:设对角线AC、BD相交于O点,
∵四边形ABCD是平行四边形,
∴$\overrightarrow{AC}$=2$\overrightarrow{AO}$=2($\overrightarrow{AP}$+$\overrightarrow{PO}$),
因此,$\overrightarrow{AP}•\overrightarrow{AC}$=$\overrightarrow{AP}•2\overrightarrow{AO}$=2$\overrightarrow{AP}•\overrightarrow{AO}$
=2$\overrightarrow{AP}$•($\overrightarrow{AP}$+$\overrightarrow{PO}$)=2${\overrightarrow{AP}}^{2}$+2$\overrightarrow{AP}$•$\overrightarrow{PO}$,
∵$\overrightarrow{|AP|}$=3,$\overrightarrow{AP}$⊥$\overrightarrow{PO}$,
∴$\overrightarrow{AP}$2=$\overrightarrow{|AP|}$2=9,$\overrightarrow{AP}$•$\overrightarrow{PO}$=0,
由此可得$\overrightarrow{AP}•\overrightarrow{AC}$=2${\overrightarrow{AP}}^{2}$+0=2×9=18.
故选:D
点评 本题在平行四边形中求向量的数量积,着重考查了平行四边形的性质、向量的线性运算性质、向量的数量积及其运算性质等知识,属于中档题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.85 | B. | 0.75 | C. | 0.8 | D. | 0.8192 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=2sin(2x-$\frac{π}{3}}$),x∈R.
已知函数f(x)=2sin(2x-$\frac{π}{3}}$),x∈R.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{3}$ln6,ln2] | B. | (-ln2,-$\frac{1}{3}$ln6) | C. | (-ln2,-$\frac{1}{3}$ln6] | D. | (-$\frac{1}{3}$ln6,ln2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com