
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|≤ ![]() ),x=﹣
),x=﹣ ![]() 为f(x)的零点,x=
为f(x)的零点,x= ![]() 为y=f(x)图象的对称轴,且f(x)在(
为y=f(x)图象的对称轴,且f(x)在( ![]() ,
, ![]() )单调,则ω的最大值为 .
)单调,则ω的最大值为 .
【答案】9
【解析】解:∵函数f(x)=sin(ωx+φ)(ω>0,|φ|≤ ![]() ),x=﹣
),x=﹣ ![]() 为f(x)的零点,x=
为f(x)的零点,x= ![]() 为y=f(x)图象的对称轴,
为y=f(x)图象的对称轴,
∴ω(﹣ ![]() )+φ=nπ,n∈Z,且ω
)+φ=nπ,n∈Z,且ω ![]() +φ=n′π+
+φ=n′π+ ![]() ,n′∈Z,
,n′∈Z,
∴相减可得ω ![]() =(n′﹣n)π+
=(n′﹣n)π+ ![]() =kπ+
=kπ+ ![]() ,k∈Z,即ω=2k+1,即ω为奇数.
,k∈Z,即ω=2k+1,即ω为奇数.
∵f(x)在( ![]() ,
, ![]() )单调,(1)若f(x)在(
)单调,(1)若f(x)在( ![]() ,
, ![]() )单调递增,
)单调递增,
则ω ![]() +φ≥2kπ﹣
+φ≥2kπ﹣ ![]() ,且ω
,且ω ![]() +φ≤2kπ+
+φ≤2kπ+ ![]() ,k∈Z,
,k∈Z,
即﹣ω ![]() ﹣φ≤﹣2kπ+
﹣φ≤﹣2kπ+ ![]() ①,且ω
①,且ω ![]() +φ≤2kπ+
+φ≤2kπ+ ![]() ,k∈Z ②,
,k∈Z ②,
把①②可得 ![]() ωπ≤π,∴ω≤12,故有奇数ω的最大值为11.
ωπ≤π,∴ω≤12,故有奇数ω的最大值为11.
当ω=11时,﹣ ![]() +φ=kπ,k∈Z,∵|φ|≤
+φ=kπ,k∈Z,∵|φ|≤ ![]() ,∴φ=﹣
,∴φ=﹣ ![]() .
.
此时f(x)=sin(11x﹣ ![]() )在(
)在( ![]() ,
, ![]() )上不单调,不满足题意.
)上不单调,不满足题意.
当ω=9时,﹣ ![]() +φ=kπ,k∈Z,∵|φ|≤
+φ=kπ,k∈Z,∵|φ|≤ ![]() ,∴φ=
,∴φ= ![]() ,
,
此时f(x)=sin(9x+ ![]() )在(
)在( ![]() ,
, ![]() )上单调递减,不满足题意;
)上单调递减,不满足题意;
故此时ω无解.(2)若f(x)在( ![]() ,
, ![]() )单调递减,
)单调递减,
则ω ![]() +φ≥2kπ+
+φ≥2kπ+ ![]() ,且ω
,且ω ![]() +φ≤2kπ+
+φ≤2kπ+ ![]() ,k∈Z,
,k∈Z,
即﹣ω ![]() ﹣φ≤﹣2kπ﹣
﹣φ≤﹣2kπ﹣ ![]() ③,且ω
③,且ω ![]() +φ≤2kπ+
+φ≤2kπ+ ![]() ,k∈Z ④,
,k∈Z ④,
把③④可得 ![]() ωπ≤π,∴ω≤12,故有奇数ω的最大值为11.
ωπ≤π,∴ω≤12,故有奇数ω的最大值为11.
当ω=11时,﹣ ![]() +φ=kπ,k∈Z,∵|φ|≤
+φ=kπ,k∈Z,∵|φ|≤ ![]() ,∴φ=﹣
,∴φ=﹣ ![]() .
.
此时f(x)=sin(11x﹣ ![]() )在(
)在( ![]() ,
, ![]() )上不单调,不满足题意.
)上不单调,不满足题意.
当ω=9时,﹣ ![]() +φ=kπ,k∈Z,∵|φ|≤
+φ=kπ,k∈Z,∵|φ|≤ ![]() ,∴φ=
,∴φ= ![]() ,
,
此时f(x)=sin(9x+ ![]() )在(
)在( ![]() ,
, ![]() )上单调递减,满足题意;
)上单调递减,满足题意;
故ω的最大值为9.
所以答案是:9.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() (a>0,b>0)上的点P到左、右两焦点F1 , F2的距离之和为2
(a>0,b>0)上的点P到左、右两焦点F1 , F2的距离之和为2 ![]() ,离心率为
,离心率为 ![]() .
.
(1)求椭圆的方程;
(2)是否存在同时满足①②两个条件的直线l?
①过点M(0, ![]() );
);
②存在椭圆上与右焦点F2共线的两点A、B,且A、B关于直线l对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,E为棱SC的中点,若AC=2 ![]() ,SA=SB=AB=BC=SC=2,则异面直线AC与BE所成的角为( )
,SA=SB=AB=BC=SC=2,则异面直线AC与BE所成的角为( ) 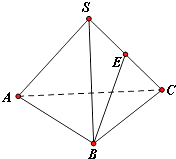
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
(1)利用计算机产生0~1之间的均匀随机数a,则事件“3a﹣1>0”发生的概率为 ![]() ;
;
(2)“x+y≠0”是“x≠1或y≠﹣1”的充分不必要条件;
(3)如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β;
(4)设 ![]() 是非零向量,已知命题p:若
是非零向量,已知命题p:若 ![]() ,
, ![]() ,则
,则 ![]() ;命题q:若
;命题q:若 ![]() ,则
,则 ![]() ,则“p∨q”是真命题.
,则“p∨q”是真命题.
其中说法正确的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)对任意的x都有f(x+2)﹣f(x)=﹣4x+4,且f(0)=0.
(1)求函数f(x)的解析式;
(2)设函数g(x)=f(x)+m,(m∈R). ①若存在实数a,b(a<b),使得g(x)在区间[a,b]上为单调函数,且g(x)取值范围也为[a,b],求m的取值范围;
②若函数g(x)的零点都是函数h(x)=f(f(x))+m的零点,求h(x)的所有零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头,它们在一昼夜内任何时刻到达是等可能的.
(1)已知甲船上有男女乘客各3名,现从中任选3人出来做某件事情,求所选出的人中恰有一位女乘客的概率;
(2)如果甲船的停泊时间为4小时,乙船的停泊时间为2小时,求它们中的任何一条船不需要等待码头空出的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(﹣∞,+∞)上的奇函数,当x>0时,f(x)=4x﹣x2 , 若函数f(x)在区间[t,4]上的值域为[﹣4,4],则实数t的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,角A、B、C的对边分别为a、b、c.已知(a+c)2﹣b2=3ac
(1)求角B;
(2)当b=6,sinC=2sinA时,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com