考点:数列递推式,数列的应用
专题:等差数列与等比数列
分析:(1)根据an2,2S,an+12成等比数列结合an>0得到2Sn=anan+1,由此得到an+1-an-1=2.说明数列的奇数项和偶数项均构成等差数列,得到数列{an}是首项为1公差为1的等差数列.则数列的通项公式可求;
(2)把{an}的通项公式代入Tn=2an-bn,整理后构造等比数列{bn-2},求出其通项公式后得答案.
解答:
解:(1)由a
n2,2S
n,a
n+12成等比数列,得
4Sn2=an2an+12.
又a
n>0,∴2S
n=a
na
n+1,则2a
1=a
1a
2,
又a
1=1,∴a
2=2.
当n>1时,2S
n-1=a
n-1a
n.
∴2a
n=a
n(a
n+1-a
n-1),即a
n+1-a
n-1=2.
∵a
1=1,a
2=2,
∴a
1,a
3,a
5,…成首项为1,公差为2的等差数列.
a
2,a
4,a
6,…成首项为2公差为2的等差数列.
∴数列{a
n}是首项为1公差为1的等差数列.
∴a
n=n;
(2)∵T
n=2a
n-b
n=2n-b
n,
∴b
1=2-b
1,b
1=1.
n>1时,T
n-1=2(n-1)-b
n-1,
∴b
n=2-b
n+b
n-1,
2b
n=2+b
n-1,
∴2(b
n-2)=b
n-1-2.
∴{b
n-2}是首项为1-2=-1,公比为
的等比数列.
∴
bn-2=-()n-1.
则
bn=2-.
点评:本题考查了数列递推式,考查了等差关系和等比关系的确定,训练了数列构造法,是中档题.



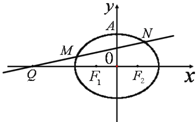 如图,已知椭圆C:
如图,已知椭圆C: