
【题目】下列命题:
①函数![]() 的最小正周期是
的最小正周期是![]() ;
;
②在直角坐标系![]() 中,点
中,点![]() ,将向量
,将向量![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到向量
得到向量![]() ,则点
,则点![]() 的坐标是
的坐标是![]() ;
;
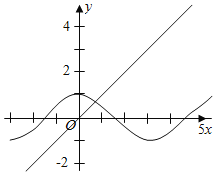
③在同一直角坐标系中,函数![]() 的图象和函数
的图象和函数![]() 的图象有两个公共点;
的图象有两个公共点;
④函数![]() 在
在![]() 上是增函数.
上是增函数.
其中,正确的命题是________(填正确命题的序号).
【答案】①②④
【解析】
由余弦函数的周期公式可判断①;由任意角的三角函数定义可判断②;由余弦函数和一次函数的图象可判断③;由诱导公式和余弦函数的单调性可判断④.
函数y=cos(﹣2x)即y=cos2x的最小正周期是π,故①正确;
在直角坐标系xOy中,点P(a,b),
将向量![]() 绕点O逆时针旋转90°得到向量
绕点O逆时针旋转90°得到向量![]() ,
,
设a=rcosα,b=rsinα,可得rcos(90°+α)=﹣rsinα=﹣b,
rsin(90°+α)=rcosα=a,则点Q的坐标是(﹣b,a),故②正确;
在同一直角坐标系中,函数y=cosx的图象和函数y=x的图象有一个公共点,故③错误;
函数y=sin(x![]() )即y=﹣cosx在[0,π]上是增函数,故④正确.
)即y=﹣cosx在[0,π]上是增函数,故④正确.
故答案为:①②④.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是()
A. 锐角是第一象限的角,所以第一象限的角都是锐角;
B. 如果向量![]() ,则
,则![]() ;
;
C. 在![]() 中,记
中,记![]() ,
,![]() ,则向量
,则向量![]() 与
与![]() 可以作为平面ABC内的一组基底;
可以作为平面ABC内的一组基底;
D. 若![]() ,
,![]() 都是单位向量,则
都是单位向量,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
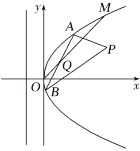
【题目】如图所示,在直角坐标系![]() 中,点
中,点![]() 到抛物线
到抛物线![]() 的准线的距离为
的准线的距离为![]() .点
.点![]() 是
是![]() 上的定点,
上的定点,![]() ,
,![]() 是
是![]() 上的两动点,且线段
上的两动点,且线段![]() 的中点
的中点![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求曲线![]() 的方程及
的方程及![]() 的值;
的值;
(Ⅱ)记![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A={x|2x2+ax+2=0},B={x|x2+3x+2a=0},且A∩B={2}.
(1)求a的值及集合A,B;
(2)设全集U=A∪B,求(UA)∪(UB);
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 与
与![]() 相交于
相交于![]() 两点,求过
两点,求过![]() 两点且面积最小的圆的标准方程.
两点且面积最小的圆的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为正整数,集合
为正整数,集合![]() (
(![]() ),对于集合
),对于集合![]() 中的任意元素
中的任意元素![]() 和
和![]() ,记
,记![]() .
.
(1)当![]() 时,若
时,若![]() ,
,![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)当![]() 时,设
时,设![]() 是
是![]() 的子集,且满足:对于
的子集,且满足:对于![]() 中的任意元素
中的任意元素![]() 、
、![]() ,当
,当![]() 、
、![]() 相同时,
相同时,![]() 是奇数,当
是奇数,当![]() 、
、![]() 不同时,
不同时,![]() 是偶数,求集合
是偶数,求集合![]() 中元素个数的最大值.
中元素个数的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(2,2),圆C:x2+y2-8y=0,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.
(1)求M的轨迹方程;
(2)当|OP|=|OM|时,求l的方程及△POM的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com