
| 不患肺癌 | 患肺癌 | 总计 | |
| 不吸烟 | 7775 | 42 | 7817 |
| 吸烟 | d | ||
| 总计 | 9874 | 9965 |
| A. | 48 | B. | 49 | C. | 50 | D. | 51 |
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当x=y=a时,数列{an}有最大值$\frac{a}{2}$ | |
| B. | 设bn=an+1-an(n∈N*),则数列{bn}为递减数列 | |
| C. | 对任意的n∈N*,始终有${a_n}≤\frac{xy}{z}$ | |
| D. | 对任意的n∈N*,都有${a_n}≤\frac{xy}{x+y}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份200x(年) | 0 | 1 | 2 | 3 | 4 |
| 人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
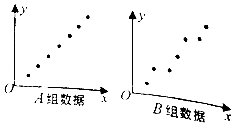 如图,给出了样本容量均为7的A、B两组样本数据的散点图,已知A组样本数据的相关系数为r1,B组数据的相关系数为r2,则( )
如图,给出了样本容量均为7的A、B两组样本数据的散点图,已知A组样本数据的相关系数为r1,B组数据的相关系数为r2,则( )| A. | r1>r2>0 | B. | r2>r1>0 | C. | r1<r2<0 | D. | r2<r1<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com