
【题目】下列命题中,正确命题的个数是( )
①若2b=a+c,则a,b,c成等差数列;
②“a,b,c成等比数列”的充要条件是“b2=ac”;
③若数列{an2}是等比数列,则数列{an}也是等比数列;
④若![]() ,则
,则![]()
A.3B.2C.1D.0
科目:高中数学 来源: 题型:
【题目】某消费品企业销售部对去年各销售地的居民年收入(即此地所有居民在一年内的收入的总和)及其产品销售额进行抽样分析,收集数据整理如下:
销售地 | A | B | C | D |
年收入x(亿元) | 15 | 20 | 35 | 50 |
销售额y(万元) | 16 | 20 | 40 | 48 |
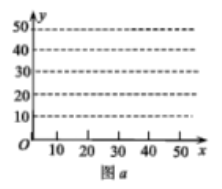
(1)在图a中作出这些数据的散点图,并指出y与x成正相关还是负相关?
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程?
(3)若B地今年的居民年收入将增长20%,预测B地今年的销售额将达到多少万元?
回归方程系数公式: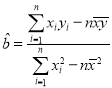 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,短轴长是2.
,短轴长是2.
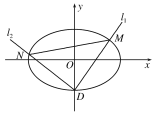
(1)求椭圆C的方程;
(2)设椭圆C的下顶点为D,过点D作两条互相垂直的直线l1,l2,这两条直线与椭圆C的另一个交点分别为M,N.设l1的斜率为k(k≠0),△DMN的面积为S,当![]() ,求k的取值范围.
,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解用户对其产品的满意度,从![]() 两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到
两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到![]() 地区用户满意度评分的频率分布直方图和
地区用户满意度评分的频率分布直方图和![]() 地区用户满意度评分的频数分布表.
地区用户满意度评分的频数分布表.
![]() 地区用户满意度评分的频率分布直方图如下:
地区用户满意度评分的频率分布直方图如下:
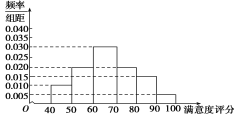
![]() 地区用户满意度评分的频数分布表如下:
地区用户满意度评分的频数分布表如下:

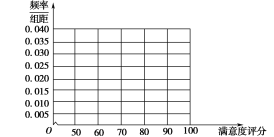
(1)在图中作出![]() 地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可).
地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可).
![]() 地区用户满意度评分的频率分布直方图
地区用户满意度评分的频率分布直方图
(2)根据用户满意度评分,将用户的满意度分为三个等级:
![]()
公司负责人为了解用户满意度情况,从B地区调查8户,其中有两户满意度等级是不满意.求从这8户中随机抽取2户检查,抽到不满意用户的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型工厂招聘到一大批新员工.为了解员工对工作的熟练程度,从中随机抽取100人组成样本,统计他们每天加工的零件数,得到如下数据:

将频率作为概率,解答下列问题:
(1)当![]() 时,从全体新员工中抽取2名,求其中恰有1名日加工零件数达到240及以上的概率;
时,从全体新员工中抽取2名,求其中恰有1名日加工零件数达到240及以上的概率;
(2)若根据上表得到以下频率分布直方图,估计全体新员工每天加工零件数的平均数为222个,求![]() 的值(每组数据以中点值代替);
的值(每组数据以中点值代替);
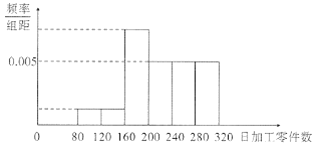
(3)在(2)的条件下,工厂按工作熟练度将新员工分为三个等级:日加工零件数未达200的员工为C级;达到200但未达280的员工为B级;其他员工为A级.工厂打算将样本中的员工编入三个培训班进行全员培训:A,B,C三个等级的员工分别参加高级、中级、初级培训班,预计培训后高级、中级、初级培训班的员工每人的日加工零件数分别可以增加20,30,50.现从样本中随机抽取1人,其培训后日加工零件数增加量为X,求随机变量X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面ABCD⊥平面CDEF,且四边形ABCD是梯形,四边形CDEF是矩形,∠BAD=∠CDA=90°,AB=AD=DE=![]() CD,M是线段DE上的动点.
CD,M是线段DE上的动点.
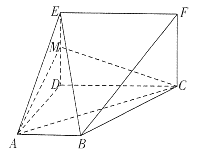
(1)试确定点M的位置,使BE∥平面MAC,并说明理由;
(2)在(1)的条件下,四面体E-MAC的体积为3,求线段AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某校学生课外时间的分配情况,拟采用分层抽样的方法从该校的高一、高二、高三这三个年级中共抽取5个班进行调查,已知该校的高一、高二、高三这三个年级分别有18、6、6个班级.
(Ⅰ)求分别从高一、高二、高三这三个年级中抽取的班级个数;
(Ⅱ)若从抽取的5个班级中随机抽取2个班级进行调查结果的对比,求这2个班级中至少有1个班级来自高一年级的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com