
【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,短轴长是2.
,短轴长是2.
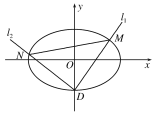
(1)求椭圆C的方程;
(2)设椭圆C的下顶点为D,过点D作两条互相垂直的直线l1,l2,这两条直线与椭圆C的另一个交点分别为M,N.设l1的斜率为k(k≠0),△DMN的面积为S,当![]() ,求k的取值范围.
,求k的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由e=![]() ,2b=2,a2=b2+c2构造方程组,解出a,b即可得椭圆方程;(2)设l1的方程为y=kx-1代入椭圆方程,求出M的坐标,可得|DM|,用
,2b=2,a2=b2+c2构造方程组,解出a,b即可得椭圆方程;(2)设l1的方程为y=kx-1代入椭圆方程,求出M的坐标,可得|DM|,用![]() 代替k,可得|DN|,求出△DMN的面积S,可得
代替k,可得|DN|,求出△DMN的面积S,可得![]() ,解不等式
,解不等式![]() >
>![]() 可得k的取值范围.
可得k的取值范围.
(1)设椭圆C的半焦距为c,则由题意得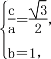 又a2=b2+c2,解得a=2,b=1,
又a2=b2+c2,解得a=2,b=1,
∴椭圆方程为![]() +y2=1.
+y2=1.
(2)由(1)知,椭圆C的方程为![]() +y2=1,
+y2=1,
所以椭圆C与y轴负半轴交点为D(0,-1).
因为l1的斜率存在,所以设l1的方程为y=kx-1.
代入![]() +y2=1,得M
+y2=1,得M![]() ,
,
从而|DM|=![]() =
=![]() .
.
用-![]() 代替k得|DN|=
代替k得|DN|=![]() .
.
所以△DMN的面积S=![]() ·
·![]() ×
×![]() =
=![]() .
.
则![]() =
=![]() ,
,
因为![]() >
>![]() ,即
,即![]() >
>![]() ,
,
整理得4k4-k2-14<0,解得-![]() <k2<2,
<k2<2,
所以0<k2<2,即-![]() <k<0或0<k<
<k<0或0<k<![]() .
.
从而k的取值范围为(-![]() ,0)∪(0,
,0)∪(0,![]() ).
).


科目:高中数学 来源: 题型:
【题目】某大学毕业生参加一个公司的招聘考试,考试分笔试和面试两个环节,笔试有![]() 、
、![]() 两个题目,该学生答对
两个题目,该学生答对![]() 、
、![]() 两题的概率分别为
两题的概率分别为![]() 、
、![]() ,两题全部答对方可进入面试.面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为
,两题全部答对方可进入面试.面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为![]() ,至少答对一个问题即可被聘用,若只答对一问聘为职员,答对两问聘为助理(假设每个环节的每个题目或问题回答正确与否是相互独立的).
,至少答对一个问题即可被聘用,若只答对一问聘为职员,答对两问聘为助理(假设每个环节的每个题目或问题回答正确与否是相互独立的).
(1)求该学生被公司聘用的概率;
(2)设该学生应聘结束后答对的题目或问题的总个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() ),以椭圆内一点
),以椭圆内一点![]() 为中点作弦
为中点作弦![]() ,设线段
,设线段![]() 的中垂线与椭圆相交于
的中垂线与椭圆相交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆的离心率;
(Ⅱ)试判断是否存在这样的![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() ,
, ![]() 在同一个圆上,并说明理由.
在同一个圆上,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确命题的个数是( )
①若2b=a+c,则a,b,c成等差数列;
②“a,b,c成等比数列”的充要条件是“b2=ac”;
③若数列{an2}是等比数列,则数列{an}也是等比数列;
④若![]() ,则
,则![]()
A.3B.2C.1D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() 与向量
与向量![]() 的对应关系用
的对应关系用![]() 表示.
表示.
(1) 证明:对于任意向量![]() 、
、![]() 及常数m、n,恒有
及常数m、n,恒有![]() ;
;
(2) 证明:对于任意向量![]() ,
,![]() ;
;
(3) 证明:对于任意向量![]() 、
、![]() ,若
,若![]() ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中, 正确说法的个数是( )
①在用![]() 列联表分析两个分类变量
列联表分析两个分类变量![]() 与
与![]() 之间的关系时,随机变量
之间的关系时,随机变量![]() 的观测值
的观测值![]() 越大,说明“A与B有关系”的可信度越大
越大,说明“A与B有关系”的可信度越大
②以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() ,
,![]() 的值分别是
的值分别是![]() 和 0.3
和 0.3
③已知两个变量具有线性相关关系,其回归直线方程为![]() ,若
,若![]() ,
,![]() ,
,![]() ,则
,则![]()
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com