
【题目】已知椭圆![]() (
(![]() ),以椭圆内一点
),以椭圆内一点![]() 为中点作弦
为中点作弦![]() ,设线段
,设线段![]() 的中垂线与椭圆相交于
的中垂线与椭圆相交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆的离心率;
(Ⅱ)试判断是否存在这样的![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() ,
, ![]() 在同一个圆上,并说明理由.
在同一个圆上,并说明理由.
科目:高中数学 来源: 题型:
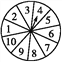
【题目】有一个转盘游戏,转盘被平均分成10等份(如图所示),转动转盘,当转盘停止后,指针指向的数字即为转出的数字.游戏规则如下:两个人参加,先确定猜数方案,甲转动转盘,乙猜,若猜出的结果与转盘转出的数字所表示的特征相符,则乙获胜,否则甲获胜.猜数方案从以下三种方案中选一种:
A.猜“是奇数”或“是偶数”
B.猜“是4的整数倍数”或“不是4的整数倍数”
C.猜“是大于4的数”或“不是大于4的数”
请回答下列问题:
(1)如果你是乙,为了尽可能获胜,你将选择哪种猜数方案,并且怎样猜?为什么?
(2)为了保证游戏的公平性,你认为应制定哪种猜数方案?为什么?
(3)请你设计一种其他的猜数方案,并保证游戏的公平性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:

(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.
附:  ,
, ![]() .
.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)若![]() 和
和![]() 在
在![]() 有相同的单调区间,求
有相同的单调区间,求![]() 的取值范围;
的取值范围;
(Ⅱ)令![]() (
(![]() ),若
),若![]() 在定义域内有两个不同的极值点.
在定义域内有两个不同的极值点.
(i)求![]() 的取值范围;
的取值范围;
(ii)设两个极值点分别为![]() ,
, ![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校要用甲、乙、丙三辆校车把教职工从老校区接到校本部,已知从老校区到校本部有两条公路,校车走公路①时堵车的概率为![]() ,校车走公路②时堵车的概率为p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆校车是否堵车相互之间没有影响.
,校车走公路②时堵车的概率为p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆校车是否堵车相互之间没有影响.
(1)若三辆校车中恰有一辆校车被堵的概率为![]() ,求走公路②堵车的概率;
,求走公路②堵车的概率;
(2)在(1)的条件下,求三辆校车中被堵车辆的辆数ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
⑴求椭圆![]() 的标准方程;
的标准方程;
⑵已知动直线![]() 过点
过点![]() 且与椭圆
且与椭圆![]() 交于
交于![]() 两点.试问
两点.试问![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系.已知曲线
轴的正半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .倾斜角为
.倾斜角为![]() ,且经过定点
,且经过定点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(Ⅰ)写出直线![]() 的参数方程的标准形式,并求曲线
的参数方程的标准形式,并求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:

(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)用二次函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程:
的关系,可得回归方程: ![]() ,计算二次函数回归模型和线性回归模型的
,计算二次函数回归模型和线性回归模型的![]() 分别约为0.75和0.97,请用
分别约为0.75和0.97,请用![]() 说明选择个回归模型更合适,并用此模型预测
说明选择个回归模型更合适,并用此模型预测![]() 超市广告费支出为8万元时的销售额.
超市广告费支出为8万元时的销售额.
参考数据:  .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com