
【题目】给出以下四个命题,其中所有真命题的序号为 .
①函数 ![]() 在区间
在区间 ![]() 上存在一个零点,则
上存在一个零点,则 ![]() 的取值范围是
的取值范围是 ![]() ;
;
②“ ![]() ”是“
”是“ ![]() 成等比数列”的必要不充分条件;
成等比数列”的必要不充分条件;
③ ![]() ,
, ![]() ;
;
④若 ![]() ,则
,则 ![]() .
.
【答案】②③④
【解析】①,∵ ![]() 在区间(1,1)上存在一个零点,
在区间(1,1)上存在一个零点,
∴ ![]() ,解得
,解得 ![]() 或
或 ![]() ,故①错误;
,故①错误;
②,若“ ![]() ”,则
”,则 ![]() 不一定成等比数列,例如
不一定成等比数列,例如 ![]() ,但“
,但“ ![]() 成等比数列”则有
成等比数列”则有 ![]() ,所以“
,所以“ ![]() ”成立,“
”成立,“ ![]() ”是“
”是“ ![]() 成等比数列”的必要不充分条件,故②正确;
成等比数列”的必要不充分条件,故②正确;
③,由图可知,单位圆O中, ![]() ,
,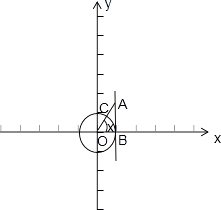
设 ![]() ,又
,又 ![]() ,
,
所以 ![]() ,故③正确;
,故③正确;
④,∵ ![]() 为增函数,
为增函数, ![]() 均为减函数,
均为减函数,
∴ ![]() ,故④正确;
,故④正确;
故答案为②③④.
根据题目中所给的条件的特点,①根据函数零点存在定理,得f(-1)f(1)<0,解不等式即可;
②利用等比数列的性质判断充分性与必要性是否成立即可;
③依题意在坐标系中画出单位圆,再利用正弦线、弧长与正切线判断;
④构造函数,利用对数函数与指数函数的单调性判断大小即可.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 ![]() 中,以
中,以 ![]() 为极点,
为极点, ![]() 轴非负半轴为极轴建立坐标系,已知曲线
轴非负半轴为极轴建立坐标系,已知曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() ,直线
,直线 ![]() 的参数方程为:
的参数方程为:  (
( ![]() 为参数),两曲线相交于
为参数),两曲线相交于 ![]() 两点.
两点.
(1)写出曲线 ![]() 的直角坐标方程和直线
的直角坐标方程和直线 ![]() 的普通方程;
的普通方程;
(2)若 ![]() 求
求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com