
【题目】在直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的上下两个焦点分别为
的上下两个焦点分别为![]() ,且
,且![]() ,椭圆过点
,椭圆过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆![]() 的一个顶点为
的一个顶点为![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于另一个点
于另一个点![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)法1:由题意可得![]() ,焦点
,焦点![]() ,
,![]() ,从而
,从而![]() ,求出a,b,由此能求出椭圆的标准方程.
,求出a,b,由此能求出椭圆的标准方程.
法2:由题意可得![]() ,焦点
,焦点![]() ,
,![]() ,椭圆过点
,椭圆过点![]() ),列方程组求出a,b,由此能求出椭圆的方程.
),列方程组求出a,b,由此能求出椭圆的方程.
法3:由题意可得![]() ,焦点
,焦点![]() ,
,![]() ,椭圆过点
,椭圆过点![]() ,得
,得![]() ,求出a,b,由此能求出椭圆的方程.
,求出a,b,由此能求出椭圆的方程.
(2)直线BF2的斜率![]() ,从而直线BF2的方程为
,从而直线BF2的方程为![]() ,联立
,联立![]() ,得点N的横坐标为
,得点N的横坐标为![]() ,由此能求出△F1BN的面积.
,由此能求出△F1BN的面积.
(1)〖解法1〗由题意可得![]() ,焦点
,焦点![]() ,
,![]()
![]() ,得
,得![]() ,
,
![]() ,
,
所以椭圆的标准方程是 ![]()
〖解法2〗由题意可得![]() ,焦点
,焦点![]() ,
,![]()
又椭圆过点![]() ,∴
,∴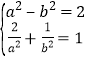
解得![]() ,
,![]()
∴椭圆的方程为![]() .
.
〖解法3〗由题意可得![]() ,焦点
,焦点![]() ,
,![]()
又椭圆过点![]() ,∴
,∴![]()
∴![]() ,∵
,∵![]() ∴可解得
∴可解得![]() ,
,![]()
∴椭圆的方程为![]() .
.
(2)![]()
![]()
![]() ,直线
,直线![]() 的斜率
的斜率![]()
直线![]() 的方程为
的方程为![]() ,即
,即![]()
联立![]() ,得点
,得点![]() 的横坐标为
的横坐标为![]()
又![]()
∴![]()
综上,![]() 的面积为
的面积为![]() .
.


科目:高中数学 来源: 题型:
【题目】某纪念章从2018年10月1日起开始上市,通过市场调查,得到该纪念章每1枚的市场价(单位:元)与上市时间(单位:天)的数据如下:
上市时间 | 4 | 10 | 36 |
市场价 | 90 | 51 | 90 |
(1)根据上表数据,从下列函数中选取一个恰当的函数描述该纪念章的市场价![]() 与上市时间
与上市时间![]() 的变化关系并说明理由:①
的变化关系并说明理由:①![]() ;②
;②![]() ;③
;③![]() .
.
(2)利用你选取的函数,求该纪念章市场价最低时的上市天数及最低的价格.
查看答案和解析>>
科目:高中数学 来源: 题型:
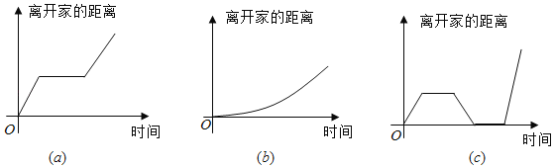
【题目】下述三个事件按顺序分别对应三个图象,正确的顺序是( )
(1)我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;(2)我骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;(3)我出发后,心情轻松,缓慢行进,后来为了赶时间开始加速.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“互联网+交通”模式的迅猛发展,“共享助力单车”在很多城市相继出现.某“共享助力单车”运营公司为了解某地区用户对该公司所提供的服务的满意度,随机调查了100名用户,得到用户的满意度评分(满分10分),现将评分分为5组,如下表:
组别 | 一 | 二 | 三 | 四 | 五 |
满意度评分 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10] |
频数 | 5 | 10 | a | 32 | 16 |
频率 | 0.05 | b | 0.37 | c | 0.16 |
(1)求表格中的a,b,c的值;
(2)估计用户的满意度评分的平均数;
(3)若从这100名用户中随机抽取25人,估计满意度评分低于6分的人数为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解华师一附中学生喜欢吃辣是否与性别有关,调研部(共10人)分三组对高中三个年级的学生进行调查,每个年级至少派3个人进行调查.(1)求调研部的甲、乙两人都被派到高一年级进行调查的概率.(2)调研部对三个年级共100人进行了调查,得到如下的列联表,请将列联表补充完整,并判断是否有![]() 以上的把握认为喜欢吃辣与性别有关?
以上的把握认为喜欢吃辣与性别有关?
喜欢吃辣 | 不喜欢吃辣 | 合计 | |
男生 | 10 | ||
女生 | 20 | 30 | |
合计 | 100 |
参考数据:

参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com