Question

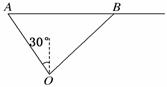
如图所示，在某港口O要将一件重要物 品用小艇送到一艘正在航行的轮船上， 在小艇出发时，轮船位于港口O北偏西 30°且与该港口相距20海里的A处，并正以30海里/小时的航行速度沿正东方向匀速行驶．假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶，经过t小时与轮船相遇．

(1)若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？

(2)为保证小艇在30分钟内(含30分钟)能与轮船相遇，试确定小艇航行速度的最小值；

Answer 1

解：(1)设相遇时小艇航行距离为S海里，则

故当t＝时，S_min＝10，v＝30，即小艇以每小时30

海里的速度航行，相遇时距离最小．

(2)若轮船与小艇在B处相遇，由题意可得：

(vt)²＝20²＋(30t)²－2·20·(30t)·cos(90°－30°)

化简得v²＝－＋900＝400²＋675，

由于0<t≤，即≥2，所以当＝2时，v取得最小值10，

即小艇航行速度的最小值为10海里/小时．