
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
已知等差数列{an}满足a2013+a2015=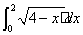 ,那么a2014(a2012+2a2014+a2016)的值为 ( )
,那么a2014(a2012+2a2014+a2016)的值为 ( )
A. B.2 C.² D.4²
查看答案和解析>>
科目:高中数学 来源: 题型:
已知曲线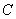 的极坐标方程为
的极坐标方程为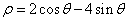 .以极点为原点,极轴为
.以极点为原点,极轴为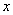 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程为
的参数方程为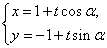 (
(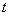 为参数).
为参数).
(Ⅰ)判断直线 与曲线
与曲线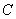 的位置关系,并说明理由;
的位置关系,并说明理由;
(Ⅱ)若直线 和曲线
和曲线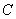 相交于
相交于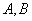 两点,且
两点,且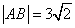 ,求直线
,求直线 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知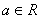 ,函数
,函数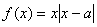 ,
,
(Ⅰ)当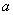 =2时,作出图形并写出函数
=2时,作出图形并写出函数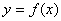 的单调递增区间;
的单调递增区间;
(Ⅱ)当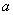 =-2时,求函数
=-2时,求函数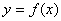 在区间
在区间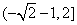 的值域;
的值域;
(Ⅲ)设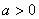 ,函数
,函数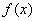 在
在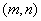 上既有最大值又有最小值,请分别求出
上既有最大值又有最小值,请分别求出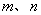 的取值范围(用
的取值范围(用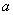 表示).
表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
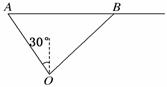 如图所示,在某港口O要将一件重要物 品用小艇送到一艘正在航行的轮船上, 在小艇出发时,轮船位于港口O北偏西 30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
如图所示,在某港口O要将一件重要物 品用小艇送到一艘正在航行的轮船上, 在小艇出发时,轮船位于港口O北偏西 30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com