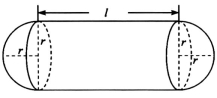
某企业拟建造如图所示的容器（不计厚度，长度单位：米），其中容器的中间为圆柱形，左右两端均为半球形，按照设计要求容器的容积为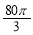
立方米，且
. 假设该容器的建造费用仅与其表面积有关. 已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为22千元. 设该容器的建造费用为y千元. 当该容器建造费用最小时，r的值为（ ）
A．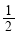
B．1 C．
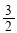D．2
科目：高中数学 来源：2013-2014学年湖北省黄冈市高三下学期三月月考文科数学试卷（解析版） 题型：选择题
下面几个命题中，假命题是（ ）
A．“若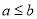
,则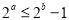
”的否命题；
B．“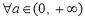
，函数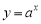
在定义域内单调递增”的否定；
C．“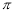
是函数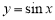
的一个周期”或“
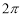是函数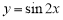
的一个周期”；
D．“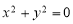
”是“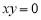
”的必要条件．
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省宜昌示范教学协作体高一下学期期中考试数学试卷（解析版） 题型：解答题
已知向量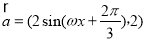
，
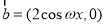
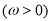，函数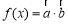
的图像与直线
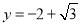的相邻两个交点之间的距离为
．
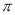（1）求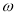
的值；
（2）求函数
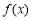在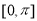
上的单调递增区间．
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省天门市毕业生四月调研考试理科数学试卷（解析版） 题型：解答题
定义：若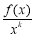
在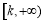
上为增函数，则称
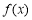为“k次比增函数”，其中
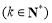. 已知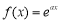
其中e为自然对数的底数.
（1）若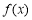是“1次比增函数”，求实数a的取值范围；
（2）当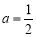
时，求函数
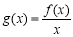在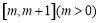
上的最小值；
（3）求证：
.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省天门市毕业生四月调研考试理科数学试卷（解析版） 题型：填空题
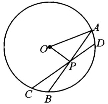
如图，AB，CD是半径为a的圆O的两条弦，它们相交于AB的中点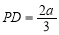P，
，
，则CP= ．
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省天门市毕业生四月调研考试理科数学试卷（解析版） 题型：选择题
设
在（
）上单调递增；
，则p是q的（ ）
A．充要条件 B．充分不必要条件 C．必要不充分条件 D．以上都不对
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省天门市毕业生四月调研考试文科数学试卷（解析版） 题型：解答题
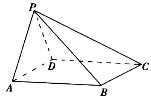
如图，在四棱锥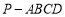
中，底面
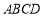为矩形，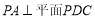
.
（1）求证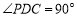
，并指出异面直线PA与CD所成角的大小；
（2）在棱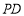
上是否存在一点
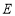，使得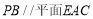
？如果存在，求出此时三棱锥
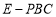与四棱锥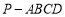的体积比；如果不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省天门市毕业生四月调研考试文科数学试卷（解析版） 题型：选择题
①若“p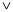
q”为真命题，则p、q均为真命题（ ）；
②“若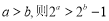
”的否命题为“若
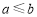，则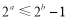
”；
③“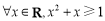
”的否定是“
”；
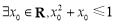④“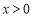
”是“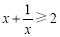
”的充要条件. 其中不正确的命题是
A．①② B．②③ C．①③ D．③④
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省七市（州）高三年级联合考试文科数学试卷（解析版） 题型：选择题
将函数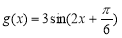
图像上所有点向左平移
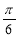个单位，再将各点横坐标缩短为原来的
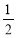倍，得到函数f(x)，则（ ）
A．f(x)在
单调递减 B．f(x)在
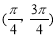单调递减
C．f(x)在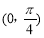
单调递增 D．f(x)在
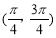单调递增
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
,由题意知：
，又 
,故
由于
,因此
.所以建造费用
,因此，
,此时易知
,故选B.
