
定义:若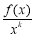 在
在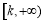 上为增函数,则称
上为增函数,则称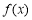 为“k次比增函数”,其中
为“k次比增函数”,其中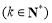 . 已知
. 已知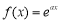 其中e为自然对数的底数.
其中e为自然对数的底数.
(1)若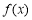 是“1次比增函数”,求实数a的取值范围;
是“1次比增函数”,求实数a的取值范围;
(2)当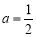 时,求函数
时,求函数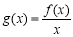 在
在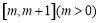 上的最小值;
上的最小值;
(3)求证: .
.
(1) 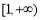 ;(2)详见解析;(3)详见解析.3.详见解析.
;(2)详见解析;(3)详见解析.3.详见解析.
【解析】
试题分析:(Ⅰ)由于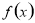 是“1次比增函数”,得到
是“1次比增函数”,得到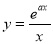 在
在 上为增函数,求导后,导数大于等于0,分离参数
上为增函数,求导后,导数大于等于0,分离参数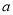 ,转化为恒成立,求最值的问题,即可得到实数a的取值范围;
,转化为恒成立,求最值的问题,即可得到实数a的取值范围;
(Ⅱ)当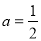 时,得到函数
时,得到函数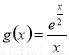 ,
, ,利用导数即可得到
,利用导数即可得到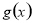 的单调区间,分成
的单调区间,分成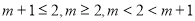 ,三种情况进行分类讨论即可函数在
,三种情况进行分类讨论即可函数在
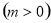 上单调性,进而得到其最小值;
上单调性,进而得到其最小值;
(Ⅲ)由(Ⅱ)当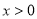 时,
时, ,即
,即 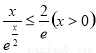 ,则
,则 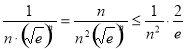 ,即可证明:
,即可证明: .,
.,
试题解析:(1)由题意知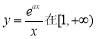 上为增函数,因为
上为增函数,因为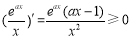 在
在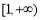 上
上
恒成立.又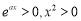 ,则
,则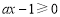 在
在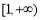 上恒成立,
上恒成立,
即 在
在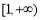 上恒成立. 而当
上恒成立. 而当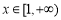 时,
时,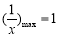 ,所以
,所以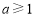 ,
,
于是实数a的取值范围是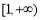 . 4分
. 4分
(2)当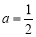 时,
时,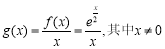 ,则
,则 .
.
当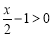 ,即
,即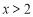 时,
时,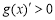 ;
;
当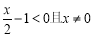 ,即
,即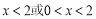 时,
时,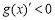 .
.
则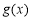 的增区间为(2,+∞),减区间为(-∞,0),(0,2). 6分
的增区间为(2,+∞),减区间为(-∞,0),(0,2). 6分
因为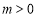 ,所以
,所以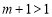 ,
,
①当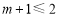 ,即
,即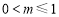 时,
时,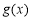 在[
在[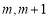 ]上单调递减,
]上单调递减,
所以 .
.
②当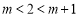 ,即
,即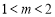 时,
时,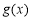 在
在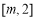 上单调递减,
上单调递减,
在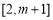 上单调递增,所以
上单调递增,所以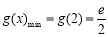 .
.
③当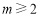 时,
时,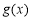 在[
在[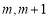 ]上单调递增,所以
]上单调递增,所以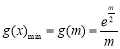 .
.
综上,当 时,
时, ;
;
当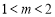 时,
时,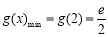 ;
;
当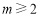 时,
时,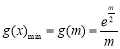 . 9分
. 9分
(3)由(2)可知,当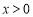 时,
时,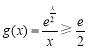 ,所以
,所以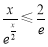
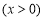 ,
,
可得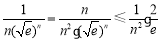 11分
11分
于是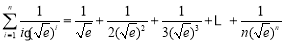
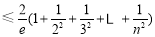
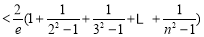

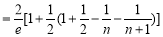
 14分
14分
考点:1.利用导数研究函数的单调性;2.利用导数求函数的最值.


科目:高中数学 来源:2013-2014学年湖北省黄冈市高三下学期三月月考文科数学试卷(解析版) 题型:填空题
设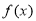 是定义在
是定义在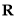 上的增函数,且对于任意的
上的增函数,且对于任意的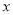 都有
都有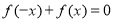 恒成立. 如果实数
恒成立. 如果实数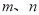 满足不等式
满足不等式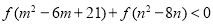 ,xxk那么
,xxk那么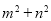 的取值范围是
的取值范围是
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省武汉市高三下学期4月调研测试文科数学试卷(解析版) 题型:选择题
在△ABC中,角A,B,C的对边分别为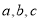 ,若A,B,C成等差数列,
,若A,B,C成等差数列,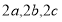 成等比数列,则
成等比数列,则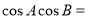 ( )
( )
A.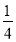 B.
B.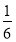 C.
C.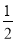 D.
D.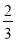
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省宜昌示范教学协作体高一下学期期中考试数学试卷(解析版) 题型:选择题
已知点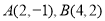 ,点
,点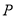 在
在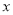 轴上,当
轴上,当 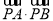 取最小值时,
取最小值时,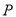 点的坐标是( )
点的坐标是( )
A.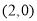 B.
B.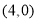 C.
C.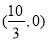 D.
D.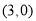
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省天门市毕业生四月调研考试理科数学试卷(解析版) 题型:解答题
设函数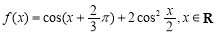 .
.
(1)求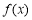 的值域;
的值域;
(2)记△ABC的内角A,B,C的对边长分别为a,b,c,若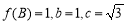 ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省天门市毕业生四月调研考试理科数学试卷(解析版) 题型:选择题
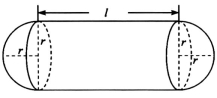
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为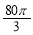 立方米,且
立方米,且 . 假设该容器的建造费用仅与其表面积有关. 已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为22千元. 设该容器的建造费用为y千元. 当该容器建造费用最小时,r的值为( )
. 假设该容器的建造费用仅与其表面积有关. 已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为22千元. 设该容器的建造费用为y千元. 当该容器建造费用最小时,r的值为( )
A.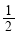 B.1 C.
B.1 C.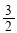 D.2
D.2
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省天门市毕业生四月调研考试文科数学试卷(解析版) 题型:填空题
分别在区间[1,6]和[1,4]内任取一个实数,依次记为m和n,则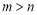 的概率为
的概率为
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试文科数学试卷(解析版) 题型:解答题
已知向量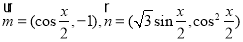 ,设函数
,设函数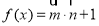 .
.
(1)求函数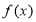 的单调递增区间;
的单调递增区间;
(2)在 中,角
中,角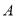 、
、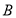 、
、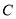 的对边分别为
的对边分别为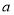 、
、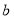 、
、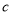 ,且满足
,且满足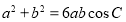 ,
,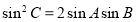 ,求
,求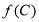 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com