
设函数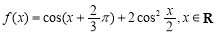 .
.
(1)求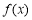 的值域;
的值域;
(2)记△ABC的内角A,B,C的对边长分别为a,b,c,若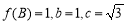 ,求a的值.
,求a的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013-2014学年湖北省黄冈市高三下学期三月月考文科数学试卷(解析版) 题型:填空题
若下框图所给的程序运行结果为S=20,那么判断框中应填入的关于整数k的条件是 。
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省武汉市高三下学期4月调研测试文科数学试卷(解析版) 题型:选择题
同时投掷两个骰子,则向上的点数之差的绝对值为4的概率是( )
A.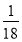 B.
B.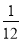 C.
C.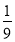 D.
D.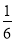
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省宜昌示范教学协作体高一下学期期中考试数学试卷(解析版) 题型:选择题
已知等比数列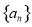 的公比为2,前4项的和是1,则前8项的和为( )
的公比为2,前4项的和是1,则前8项的和为( )
A.23 B.21 C.19 D.17
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省天门市毕业生四月调研考试理科数学试卷(解析版) 题型:解答题
定义:若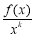 在
在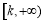 上为增函数,则称
上为增函数,则称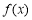 为“k次比增函数”,其中
为“k次比增函数”,其中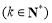 . 已知
. 已知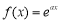 其中e为自然对数的底数.
其中e为自然对数的底数.
(1)若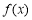 是“1次比增函数”,求实数a的取值范围;
是“1次比增函数”,求实数a的取值范围;
(2)当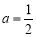 时,求函数
时,求函数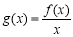 在
在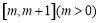 上的最小值;
上的最小值;
(3)求证: .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省天门市毕业生四月调研考试理科数学试卷(解析版) 题型:填空题
已知 展开式各项的系数和比各项的二次式系数和大992,则展开式中系数最大的项是第 项.
展开式各项的系数和比各项的二次式系数和大992,则展开式中系数最大的项是第 项.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省天门市毕业生四月调研考试理科数学试卷(解析版) 题型:选择题
设 在(
在( )上单调递增;
)上单调递增; ,则p是q的( )
,则p是q的( )
A.充要条件 B.充分不必要条件 C.必要不充分条件 D.以上都不对
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省天门市毕业生四月调研考试文科数学试卷(解析版) 题型:选择题
已知函数 是定义在R上的可导函数,其导函数记为
是定义在R上的可导函数,其导函数记为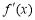 ,若对于任意实数x,有
,若对于任意实数x,有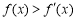 ,且
,且 为奇函数,则不等式
为奇函数,则不等式 的解集为( )
的解集为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试文科数学试卷(解析版) 题型:填空题
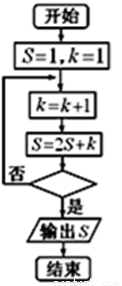
某程序框图如图所示,判断框内为“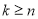 ?”,
?”,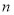 为正整数,若输出的
为正整数,若输出的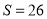 ,则判断框内的
,则判断框内的 ________;
________;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com