
已知向量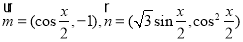 ,设函数
,设函数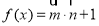 .
.
(1)求函数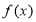 的单调递增区间;
的单调递增区间;
(2)在 中,角
中,角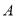 、
、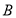 、
、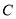 的对边分别为
的对边分别为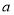 、
、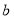 、
、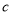 ,且满足
,且满足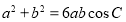 ,
,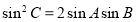 ,求
,求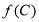 的值.
的值.
科目:高中数学 来源:2013-2014学年湖北省天门市毕业生四月调研考试理科数学试卷(解析版) 题型:解答题
定义:若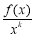 在
在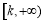 上为增函数,则称
上为增函数,则称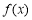 为“k次比增函数”,其中
为“k次比增函数”,其中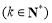 . 已知
. 已知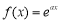 其中e为自然对数的底数.
其中e为自然对数的底数.
(1)若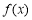 是“1次比增函数”,求实数a的取值范围;
是“1次比增函数”,求实数a的取值范围;
(2)当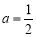 时,求函数
时,求函数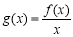 在
在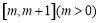 上的最小值;
上的最小值;
(3)求证: .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省天门市毕业生四月调研考试文科数学试卷(解析版) 题型:选择题
①若“p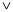 q”为真命题,则p、q均为真命题( );
q”为真命题,则p、q均为真命题( );
②“若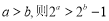 ”的否命题为“若
”的否命题为“若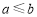 ,则
,则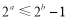 ”;
”;
③“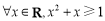 ”的否定是“
”的否定是“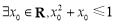 ”;
”;
④“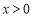 ”是“
”是“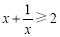 ”的充要条件. 其中不正确的命题是
”的充要条件. 其中不正确的命题是
A.①② B.②③ C.①③ D.③④
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试理科数学试卷(解析版) 题型:选择题
设两条直线的方程分别为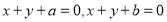 ,已知
,已知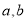 是方程
是方程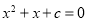 的两个实根,且
的两个实根,且 ,则这两条直线之间的距离的最大值和最小值分别是( )
,则这两条直线之间的距离的最大值和最小值分别是( )
A.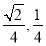 B.
B.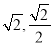 C.
C.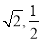 D.
D.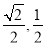
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试理科数学试卷(解析版) 题型:选择题
已知全集U=R,集合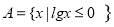 ,B=
,B=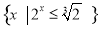 ,则A∪B=( )
,则A∪B=( )
A.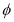 B.
B.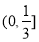 C.
C.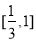 D.
D.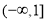
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试文科数学试卷(解析版) 题型:填空题
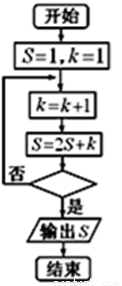
某程序框图如图所示,判断框内为“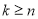 ?”,
?”,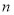 为正整数,若输出的
为正整数,若输出的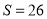 ,则判断框内的
,则判断框内的 ________;
________;
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省七市(州)高三年级联合考试文科数学试卷(解析版) 题型:选择题
将函数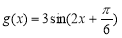 图像上所有点向左平移
图像上所有点向左平移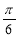 个单位,再将各点横坐标缩短为原来的
个单位,再将各点横坐标缩短为原来的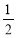 倍,得到函数f(x),则( )
倍,得到函数f(x),则( )
A.f(x)在 单调递减 B.f(x)在
单调递减 B.f(x)在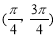 单调递减
单调递减
C.f(x)在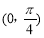 单调递增 D.f(x)在
单调递增 D.f(x)在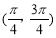 单调递增
单调递增
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三高考模拟冲刺卷(提优卷)(三)理科数学试卷(解析版) 题型:填空题
已知函数f(x)=eax-x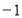 ,其中a≠0.若对一切x∈R,f(x)≥0恒成立,则a的取值集合 .
,其中a≠0.若对一切x∈R,f(x)≥0恒成立,则a的取值集合 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com