【题目】若{ 
、 
、 
}为空间的一组基底，则下列各项中，能构成基底的一组向量是（ ）
A.
， + 
， ﹣
B. ， + ， ﹣
C.
， + ， ﹣
D. + ， ﹣ ， +2
【答案】C
【解析】解：∵（ 
+ 
）+（ ﹣ ）=2 ，∴ ， + ， ﹣ 共面，不能构成基底，排除 A；∵（ + ）﹣（ ﹣ ）=2 ，∴ ， + ， ﹣ 共面，不能构成基底，排除 B；
∵ +2 = 
（ + ）﹣ 
（ ﹣ ），∴， + ， ﹣ ， +2 共面，不能构成基底，排除 D；
若 
、 + 、 ﹣ 共面，则 =λ（ + ）+m（ ﹣ ）=（λ+m） +（λ﹣m） ，则 、 、 为共面向量，此与{ 、 、 }为空间的一组基底矛盾，故 ， + ， ﹣ 可构成空间向量的一组基底．
故选：C
空间的一组基底，必须是不共面的三个向量，利用向量共面的充要条件可证明A、B、D三个选项中的向量均为共面向量，利用反证法可证明C中的向量不共面
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x2﹣2ax+5（a＞1），
（1）若f（x）的定义域和值域均是[1，a]，求实数a的值；
（2）若f（x）在区间（﹣∞，2]上是减函数，且对任意的x∈[1，a+1]，都有f（x）≤0，求实数a的取值范围；
（3）若g（x）=2x+log2（x+1），且对任意的x∈[0，1]，都存在x0∈[0，1]，使得f（x0）=g（x）成立，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线
上任意一点到直线
的距离比到点
的距离大1.
（1）求曲线
的方程；
（2）过曲线
的焦点
，且倾斜角为
的直线交
于点
（
在
轴上方），
为
的准线，点
在
上且
,求
到直线
的距离.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1，2，在Rt△ABC中，AB=BC=4，点E在线段AB上，过点E作交AC于点F，将△AEF沿EF折起到△PEF的位置（点A与P重合），使得∠PEB=60°．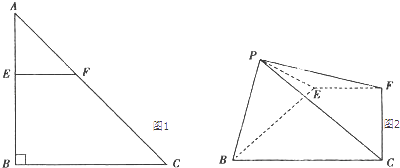 
（1）求证：EF⊥PB；
（2）试问：当点E在何处时，四棱锥P﹣EFCB的侧面的面积最大？并求此时四棱锥P﹣EFCB的体积及直线PC与平面EFCB所成角的正切值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=（ 
）x ， 函数g（x）=log 
x．
（1）若g（ax2+2x+1）的定义域为R，求实数a的取值范围；
（2）当x∈[（ ）t+1 ， （ ）t]时，求函数y=[g（x）]2﹣2g（x）+2的最小值h（t）；
（3）是否存在非负实数m，n，使得函数y=log f（x2）的定义域为[m，n]，值域为[2m，2n]，若存在，求出m，n的值；若不存在，则说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知销售“笔记本电脑”和“台式电脑”所得的利润分别是P（单位：万元）和Q（单位：万元），它们与进货资金t（单位：万元）的关系有经验公式P= 
t和Q= 
．某商场决定投入进货资金50万元，全部用来购入这两种电脑，那么该商场应如何分配进货资金，才能使销售电脑获得的利润y（单位：万元）最大？最大利润是多少万元？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列命题正确的是（ ）
A.在△ABC中，角A，B，C的对边分别是a，b，c，则a＞b是cos A＜cos B的充要条件
B.命题p：对任意的x∈R，x2+x+1＞0，则￢p：对任意的x∈R，x2+x+1≤0
C.已知p： 
＞0，则￢p： ≤0
D.存在实数x∈R，使sin x+cos x= 
成立
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
