科目：高中数学 来源： 题型：
设f(x)与g(x)是定义在同一区间[a，b]上的两个函数，若函数y＝f(x)－g(x)在x∈[a，b]上有两个不同的零点，则称f(x)和g(x)在[a，b]上是“关联函数”，区间[a，b]称为“关联区间”．若f(x)＝x2－3x＋4与g(x)＝2x＋m在[0,3]上是“关联函数”，则m的取值范围是 ( )．
A.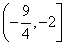 
B．[－1,0] C．(－∞，－2] D.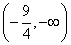 
查看答案和解析>>
科目：高中数学 来源： 题型：
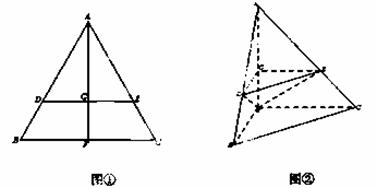
如图①，已知
ABC是边长为l的等边三角形，D，E分别是AB，AC边上的点，AD=AE，F是BC的中点，AF与DE交于点G，将ABF沿AF折起，得到如图②所示的三棱锥A-BCF，其中BC=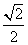
．
(1)证明：DE//平面BCF；
(2)证明：CF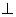
平面ABF；
(3)当AD=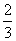
时，求三棱锥F-DEG的体积
查看答案和解析>>
科目：高中数学 来源： 题型：
已知椭圆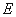
:
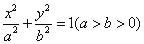的左焦点为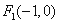
,且过点
.
(1)求椭圆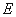的方程;
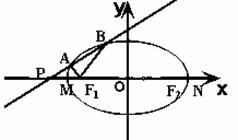
(2)设过点P(-2,0)的直线与椭圆E交于A、B两点，且满足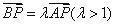
.
①若
,求
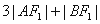的值;
②若M、N分别为椭圆E的左、右顶点，证明: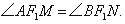 
查看答案和解析>>
科目：高中数学 来源： 题型：
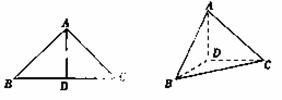
如图，在△ABC中，∠ABC＝45°，∠BAC＝90°，AD是BC上的高，沿AD把△ABD折起，使∠BDC＝90°. (1)证明：平面ADB⊥平面BDC；
(2)若BD＝1，求三棱锥DABC的表面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
是双曲线
的两个焦点, 
是
上一点,若
且
的最小内角为
,则
（B）
（C）
（D）
(i是虚数单位)，则复数z在复平面内对应的点位于( )
，以右顶点为圆心，实半轴长为半径的圆被双曲线的一条渐近线分为弧
长为1：2的两部分，则双曲线的离心率为（ ）
B. 
C. 
D. 
（
＞2）的最小值（ ）
B.
C.
D.
, 则 “
”是“
”的__________.