
分析 (1)先求导数,计算f′(1),从而求出切线方程即可;
(2)分离参数,转化为函数的最值问题求解.
解答 解:(1)∵f′(x)=1+lnx,
∴f′(1)=1=k,
故切线方程是:y=x-1;
(2)由题意,不等式化为ax≤2xlnx+x2+3,因为x>0,
所以a≤2lnx+x+$\frac{3}{x}$,当x>0时恒成立.
令h(x)=2lnx+x+$\frac{3}{x}$,则h′(x)=$\frac{2}{x}$-$\frac{3}{{x}^{2}}$+1=$\frac{(x+3)(x-1)}{{x}^{2}}$,
当0<x<1时,h′(x)<0,x>1时,h′(x)>0,
所以h(x)在(0,1)上递减,在(1,+∞)上递增.
故h(x)min=h(1)=2ln1+1+3=4.所以a≤4.
故所求a的范围是(-∞,4].
点评 本题主要考查了不等式恒成立问题的解题思路,一般此类问题转化为函数的最值问题来解.


科目:高中数学 来源: 题型:解答题
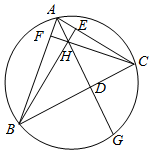 如图,已知AD、BE、CF分别是△ABC三边的高,H是垂心,AD的延长线交△ABC的外接圆于点G.
如图,已知AD、BE、CF分别是△ABC三边的高,H是垂心,AD的延长线交△ABC的外接圆于点G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组号 | 分组 | 回答 正确 的人数 | 回答正确 的人数占本 组的频率 | 频率正确直方图 |
| 第1组 | [15,25) | 5 | 0.5 | 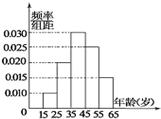 |
| 第2组 | [25,35) | a | 0.9 | |
| 第3组 | [35,45) | 27 | x | |
| 第4组 | [45,55) | 9 | 0.36 | |
| 第5组 | [55,65) | 3 | 0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
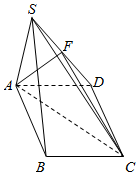 已知在四棱锥S-ABCD中,底面ABCD是菱形,且∠BCD=60°,侧面SAB是正三角形,且面SAB⊥面ABCD,F为SD的中点.
已知在四棱锥S-ABCD中,底面ABCD是菱形,且∠BCD=60°,侧面SAB是正三角形,且面SAB⊥面ABCD,F为SD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
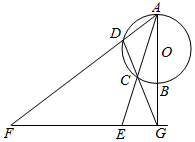 如图所示,AB是⊙O的直径,G为AB延长线上的一点,GCD是⊙O的割线,过点G作AB的垂线,交AC的延长线于点E,交AD的延长线于点F.求证:
如图所示,AB是⊙O的直径,G为AB延长线上的一点,GCD是⊙O的割线,过点G作AB的垂线,交AC的延长线于点E,交AD的延长线于点F.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com