
���� ��1��ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=-\sqrt{3}t}\\{y=\frac{2\sqrt{3}}{3}+t}\end{array}\right.$��tΪ����������ȥ����t�ɵ�ֱ��l����ͨ���̣���x=��cos�ȣ�y=��sin�ȴ�����ʽ�ɵü����귽�̣�ԲC�IJ�������Ϊ$\left\{\begin{array}{l}{x=2cos��}\\{y=2sin��}\end{array}\right.$����Ϊ������������cos2��+sin2��=1�ɵ�ֱ�����귽�̣������õ�ԲC�ļ����귽�̣�
��2������$\left\{\begin{array}{l}{��=2}\\{��cos����-\frac{��}{3}��=1}\end{array}\right.$����ã�A��B�������������������ε�������㹫ʽ�ó���
��� 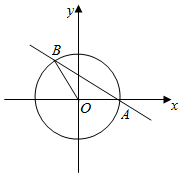 �⣺��1��ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=-\sqrt{3}t}\\{y=\frac{2\sqrt{3}}{3}+t}\end{array}\right.$��tΪ����������ȥ����tֱ��l����ͨ����Ϊ$x+\sqrt{3}y$-2=0��
�⣺��1��ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=-\sqrt{3}t}\\{y=\frac{2\sqrt{3}}{3}+t}\end{array}\right.$��tΪ����������ȥ����tֱ��l����ͨ����Ϊ$x+\sqrt{3}y$-2=0��
��x=��cos�ȣ�y=��sin�ȴ�����ʽ�ɵã���cos��+$\sqrt{3}$��sin��-2=0��
�����ֱ��l�ķ���Ϊ$��cos����-\frac{��}{3}��$=1��
ԲC�IJ�������Ϊ$\left\{\begin{array}{l}{x=2cos��}\\{y=2sin��}\end{array}\right.$����Ϊ���������ɵ�ֱ�����귽�̣�x2+y2=4���ɵ�ԲC�ļ����귽��Ϊ��=2��
��2����$\left\{\begin{array}{l}{��=2}\\{��cos����-\frac{��}{3}��=1}\end{array}\right.$����֮�ã�A��2��0����B��2��$\frac{2��}{3}$����
���AOB=$\frac{2��}{3}$����S����AOB=$\frac{1}{2}��•{r}^{2}$=$\frac{1}{2}��\frac{2��}{3}��{2}^{2}$=$\frac{4��}{3}$��
��S��AOB=$\frac{1}{2}$|OA||OB|sin��=$\sqrt{3}$��
��S=S����AOB-S��AOB=$\frac{4��}{3}$-$\sqrt{3}$��
���� ���⿼����ֱ�������뼫����Ļ������������̻�Ϊ��ͨ���̡����ߵĽ��㡢������������������㹫ʽ��������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
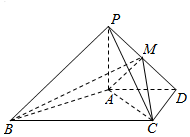 ��ͼ��������P-ABCD�У�PA��ƽ��ABCD��AD��BC����ADC=90�㣬��PA=2��AD=CD=$\frac{1}{2}$BC=2$\sqrt{2}$����M��PD�ϣ�
��ͼ��������P-ABCD�У�PA��ƽ��ABCD��AD��BC����ADC=90�㣬��PA=2��AD=CD=$\frac{1}{2}$BC=2$\sqrt{2}$����M��PD�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪������ABCDEFG����һ��ƽ��س�����ABCD-A1B1C1D1���õļ����壬��ͼ��ʾ������AB=2BC=2AF=4CG=4��
��֪������ABCDEFG����һ��ƽ��س�����ABCD-A1B1C1D1���õļ����壬��ͼ��ʾ������AB=2BC=2AF=4CG=4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | ����Ѽ�� | B�� | ��ƷѼ���� | ||
| C�� | ��ƷѼ�չ������ʡ��ӹ� | D�� | �����ӹ�������ϵ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com