
分析 画出约束条件的可行域,利用所求表达式的几何意义求解即可.
解答 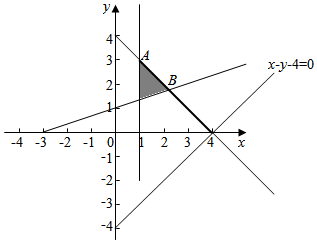 解:变量x,y满足不等式组$\left\{\begin{array}{l}x+y-4≤0\\ x-3y+3≤0\\ x≥1\end{array}$,表示的可行域如图:$\left\{\begin{array}{l}{x+y-4=0}\\{x=1}\end{array}\right.$,可得A(1,3),
解:变量x,y满足不等式组$\left\{\begin{array}{l}x+y-4≤0\\ x-3y+3≤0\\ x≥1\end{array}$,表示的可行域如图:$\left\{\begin{array}{l}{x+y-4=0}\\{x=1}\end{array}\right.$,可得A(1,3),
$\left\{\begin{array}{l}{x+y-4=0}\\{x-3y+3=0}\end{array}\right.$,可得B($\frac{9}{4}$,$\frac{7}{4}$).
z=$\frac{{|{x-y-4}|}}{{\sqrt{2}}}$的几何意义是可行域内的点到直线x-y-4=0的距离,由图形可知:A到直线的距离最大,B到直线的距离最小.
最大值为:$\frac{|1-3-4|}{\sqrt{2}}$=3$\sqrt{2}$,
最小值为:$\frac{|\frac{9}{4}-\frac{7}{4}-4|}{\sqrt{2}}$=$\frac{7\sqrt{2}}{4}$.
故答案为:$[{\frac{{7\sqrt{2}}}{4},3\sqrt{2}}]$.
点评 本题考查解得线性规划的应用,作出可行域以及表达式的几何意义是解题的关键,考查计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
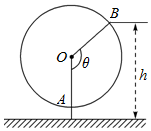 (1,3班做)一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面间的距离为h.
(1,3班做)一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面间的距离为h.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
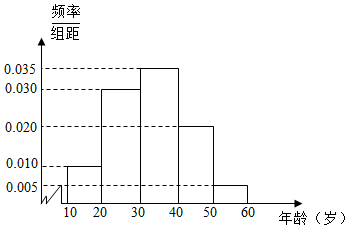 随着网络信息时代的来临,支付宝已经实现了许多功能,如购物付款、加油付款、理财产品等,使得越来越多的人在生活中使用手机支付的便捷功能,阿里巴巴公司研究人员对某地区年龄在10~60岁间的n位市民对支付宝的使用情况作出调查,并将调查的人员的年龄情况绘制成频率分布直方图如图所示.
随着网络信息时代的来临,支付宝已经实现了许多功能,如购物付款、加油付款、理财产品等,使得越来越多的人在生活中使用手机支付的便捷功能,阿里巴巴公司研究人员对某地区年龄在10~60岁间的n位市民对支付宝的使用情况作出调查,并将调查的人员的年龄情况绘制成频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {(${\frac{2}{3}$,$\frac{5}{3}})$)} | B. | ($\frac{2}{3}$,$\frac{5}{3}}$) | C. | {${\frac{2}{3}$,$\frac{5}{3}}$} | D. | {(${\frac{2}{3}$,$\frac{5}{3}}$),(-$\frac{2}{3}$,-$\frac{5}{3}}$)} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,0] | B. | [-1,2] | C. | (1,2] | D. | (-∞,1]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{2}{17}$ | C. | $\frac{3}{26}$ | D. | $\frac{3}{28}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com