
| A. | $\frac{1}{8}$ | B. | $\frac{2}{17}$ | C. | $\frac{3}{26}$ | D. | $\frac{3}{28}$ |
分析 根据题意,分2种情况讨论,甲乙其中一人参加和甲乙两人都参加,再求出甲乙相邻的有多少种情况,由此能求出甲、乙两人都发言且发言顺序不相邻的概率.
解答 解:根据题意,分2种情况讨论,
若甲乙其中一人参加,有${C}_{2}^{1}{C}_{5}^{3}{A}_{4}^{4}$=480种情况,
若甲乙两人都参加,则丙不能参加,有${C}_{2}^{2}{C}_{4}^{2}{A}_{4}^{4}$=144种情况,
其中甲乙相邻的有${C}_{2}^{2}{C}_{4}^{2}{A}_{3}^{3}{A}_{2}^{2}$=72种情况,
则甲、乙两人都发言且发言顺序不相邻的概率为P=$\frac{144-72}{480+144}$=$\frac{3}{26}$.
故选:C.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
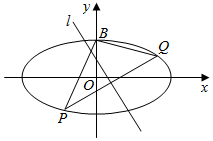 在平面直角坐标系xOy中,椭圆Γ:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,椭圆Γ上一动点M到其右焦点F(c,0)(c>0)的最小距离为2-$\sqrt{3}$.
在平面直角坐标系xOy中,椭圆Γ:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,椭圆Γ上一动点M到其右焦点F(c,0)(c>0)的最小距离为2-$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
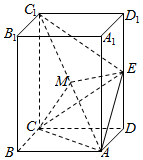 如图所示,正四棱柱ABCD-A1B1C1D1的底面边长为1,DD1=2,E为DD1的中点,连结C1E,CE,AC,AE,AC1,B1E.
如图所示,正四棱柱ABCD-A1B1C1D1的底面边长为1,DD1=2,E为DD1的中点,连结C1E,CE,AC,AE,AC1,B1E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com