
分析 根据新定义求出k元平均子集的个数,即可得出结论.
解答 解:X(S)=5,将S中的元素分成5组(1,9),(2,8),(3,7),(4,6),(5).
则fS(1)=C11=1,fS(2)=C41=4,fS(3)=C11•C41=4,fS(4)=C42=6,fS(5)=C11•C42=6,
同理:X(T)=0,将T中的元素分成5组(1,-1),(2,-2),(3,-3),(4,-4),(0).
则fT(1)=C11=1,fT(2)=C41=4,fT(3)=C11•C41=4,fT(4)=C42=6,fT(5)=C11•C42=6,
∴fS(4)+fT(5)=12.
故答案为:12.
点评 本题考查了对新定义的理解,组合数公式的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
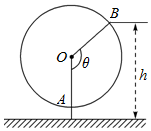 (1,3班做)一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面间的距离为h.
(1,3班做)一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面间的距离为h.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
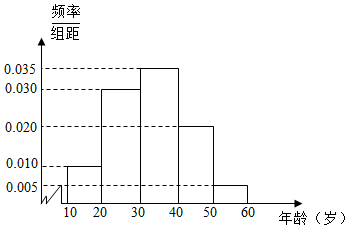 随着网络信息时代的来临,支付宝已经实现了许多功能,如购物付款、加油付款、理财产品等,使得越来越多的人在生活中使用手机支付的便捷功能,阿里巴巴公司研究人员对某地区年龄在10~60岁间的n位市民对支付宝的使用情况作出调查,并将调查的人员的年龄情况绘制成频率分布直方图如图所示.
随着网络信息时代的来临,支付宝已经实现了许多功能,如购物付款、加油付款、理财产品等,使得越来越多的人在生活中使用手机支付的便捷功能,阿里巴巴公司研究人员对某地区年龄在10~60岁间的n位市民对支付宝的使用情况作出调查,并将调查的人员的年龄情况绘制成频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{2}{17}$ | C. | $\frac{3}{26}$ | D. | $\frac{3}{28}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com