
| A. | 0 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
分析 根据重心的性质以及向量加法的平行四边形法则、向量数乘的几何意义便可得出$\overrightarrow{AP}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})$,这样根据条件进行数量积的运算便可求出$(\overrightarrow{AB}+\overrightarrow{AC})^{2}$的值,从而得出$\overrightarrow{AP}•(\overrightarrow{AB}+\overrightarrow{AC})$的值.
解答 解:如图,
根据条件:$\overrightarrow{AP}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})$;
∴$\overrightarrow{AP}•(\overrightarrow{AB}+\overrightarrow{AC})=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})^{2}$
=$\frac{1}{3}({\overrightarrow{AB}}^{2}+2\overrightarrow{AB}•\overrightarrow{AC}+{\overrightarrow{AC}}^{2})$
=$\frac{1}{3}(4+4+4)$
=4.
故选:D.
点评 考查三角形重心的概念及性质,向量数乘的几何意义,向量加法的平行四边形法则,向量的数乘运算,以及向量数量积的运算及计算公式.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
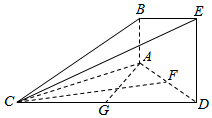 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD是等边三角形,AD=DE=2AB=2,F,G分别为AD,DC的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD是等边三角形,AD=DE=2AB=2,F,G分别为AD,DC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p∨q | B. | ¬p∧¬q | C. | p∧¬q | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com