
分析 由条件可得(a+b+c)($\frac{4}{a}$+$\frac{9}{b}$+$\frac{16}{c}$)=[($\sqrt{a}$)2+($\sqrt{b}$)2+($\sqrt{c}$)2][($\frac{2}{\sqrt{a}}$)2+($\frac{3}{\sqrt{b}}$)2+($\frac{4}{\sqrt{c}}$)2],运用柯西不等式,即可得到所求最小值,求得a=2,b=3,c=4时,取得最小值.
解答 解:a,b,c均为正数且a+b+c=9,
由柯西不等式,可得
(a+b+c)($\frac{4}{a}$+$\frac{9}{b}$+$\frac{16}{c}$)=[($\sqrt{a}$)2+($\sqrt{b}$)2+($\sqrt{c}$)2][($\frac{2}{\sqrt{a}}$)2+($\frac{3}{\sqrt{b}}$)2+($\frac{4}{\sqrt{c}}$)2]
≥($\sqrt{a}$•$\frac{2}{\sqrt{a}}$+$\sqrt{b}$•$\frac{3}{\sqrt{b}}$+$\sqrt{c}$•$\frac{4}{\sqrt{c}}$)2=(2+3+4)2=81.
当$\frac{1}{2}$a=$\frac{1}{3}$b=$\frac{1}{4}$c,即a=2,b=3,c=4时,
$\frac{4}{a}$+$\frac{9}{b}$+$\frac{16}{c}$的最小值为9.
故答案为:9.
点评 本题考查最值的求法,注意运用变形和柯西不等式,注意等号成立的条件,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
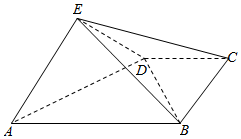 如图,四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2.
如图,四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{4}{5}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在数列{an}中,a1=1,an=$\frac{1}{2}$(an-1+$\frac{1}{{a}_{n-1}}$)(n∈N*),由其归纳出{an}的通项公式 | |
| B. | 由平面三角形的性质,推测空间四面体性质 | |
| C. | 两条直线平行,同旁内角互补,如果∠A和∠B是两条平行直线的同旁内角,则∠A+∠B=180° | |
| D. | 某校高二共10个班,1班51人,2班53人,3班52人,由此推测各班都超过50人 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com