
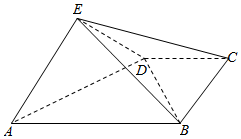
 如图,四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2.
如图,四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2.分析 (1)由勾股定理得出AD=BD=2$\sqrt{2}$,故而AD⊥BD,由面面垂直的性质得出BD⊥平面ADE;
(2)以D为原点建立坐标系,求出$\overrightarrow{BE}$和平面CDE的法向量$\overrightarrow{n}$,则直线BE和平面CDE所成角的正弦值为|cos<$\overrightarrow{n},\overrightarrow{BE}$>|.
解答 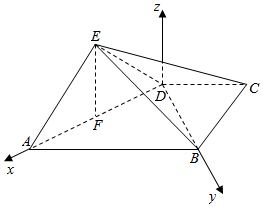 解:(1)∵EA=ED=2,EA⊥ED,∴AD=2$\sqrt{2}$.
解:(1)∵EA=ED=2,EA⊥ED,∴AD=2$\sqrt{2}$.
∵BC=CD=2,BC⊥CD,∴BD=2$\sqrt{2}$
又AB=4,∴AD2+BD2=AB2,∴AD⊥BD.
又平面EAD⊥平面ABCD,平面EAD∩平面ABCD=AD,BD?平面ABCD,
∴BD⊥平面ADE.
(2)取AD的中点F,连接EF,则EF⊥平面ABCD,EF=$\sqrt{2}$.
过D点作直线Oz∥EF,则Oz⊥平面ABCD.
以D为坐标原点,以DA,DB,Dz为坐标轴建立空间直角坐标系D-xyz,
∴D(0,0,0),C(-$\sqrt{2}$,$\sqrt{2}$,0),B(0,2$\sqrt{2}$,0),E($\sqrt{2}$,0,$\sqrt{2}$),
∴$\overrightarrow{BE}$=($\sqrt{2}$,-2$\sqrt{2}$,$\sqrt{2}$),$\overrightarrow{DE}$=($\sqrt{2}$,0,$\sqrt{2}$),$\overrightarrow{DC}$=(-$\sqrt{2}$,$\sqrt{2}$,0).
设平面CDE的一个法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DE}=0}\\{\overrightarrow{n}•\overrightarrow{DC}=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{\sqrt{2}x+\sqrt{2}z=0}\\{-\sqrt{2}x+\sqrt{2}y=0}\end{array}\right.$,设x=1得$\overrightarrow{n}$=(1,1,-1).
∴cos<$\overrightarrow{n},\overrightarrow{BE}$>=$\frac{\overrightarrow{n}•\overrightarrow{BE}}{|\overrightarrow{n}||\overrightarrow{BE}|}$=$\frac{-2\sqrt{2}}{\sqrt{3}•2\sqrt{3}}$=-$\frac{\sqrt{2}}{3}$.
∴直线BE和平面CDE所成角的正弦值为$\frac{\sqrt{2}}{3}$.
点评 本题考查了线面垂直的判定,空间向量的应用与线面角的计算,属于中档题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{32π}{3}$ | B. | $\frac{16\sqrt{7}π}{3}$ | C. | $\frac{33π}{2}$ | D. | $\frac{11\sqrt{7}π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{e-2}{2e}$) | B. | ($\frac{e-2}{2e}$,$\frac{e-1}{e}$) | C. | ($\frac{e-1}{e}$,$\frac{{{e^2}-1}}{e}$) | D. | ($\frac{{{e^2}-1}}{e}$,$\frac{{2{e^2}-1}}{e}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com