
| A. | (0,$\frac{e-2}{2e}$) | B. | ($\frac{e-2}{2e}$,$\frac{e-1}{e}$) | C. | ($\frac{e-1}{e}$,$\frac{{{e^2}-1}}{e}$) | D. | ($\frac{{{e^2}-1}}{e}$,$\frac{{2{e^2}-1}}{e}$) |
分析 分别设出切线l1、l2的切点,求得函数的导数,可得切线的斜率,以及切线的方程,结合两点的斜率公式,可得a=$\frac{1}{{x}_{1}}$-$\frac{1}{e}$.消去a,可得lnx1-1+$\frac{1}{{x}_{1}}$-$\frac{1}{e}$=0,令m(x)=lnx-1+$\frac{1}{x}$-$\frac{1}{e}$=0,求得导数,判断单调性,可得x1的范围,进而得到所求范围.
解答 解:设切线l2的方程为y=k2x,切点为(x2,y2),
则y2=ex2,k2=g′(x2)=${e}^{{x}_{2}}$=$\frac{{y}_{2}}{{x}_{2}}$,
所以x2=1,y2=e,则k2=${e}^{{x}_{2}}$=e.
由题意知,切线l1的斜率为k1=$\frac{1}{{k}_{2}}$=$\frac{1}{e}$,l1的方程为y=k1x=$\frac{1}{e}$x.
设l1与曲线y=f(x)的切点为(x1,y1),
则k1=f′(x1)=$\frac{1}{{x}_{1}}$-a=$\frac{1}{e}$=$\frac{{y}_{1}}{{x}_{1}}$,
所以y1=$\frac{{x}_{1}}{e}$=1-ax1,a=$\frac{1}{{x}_{1}}$-$\frac{1}{e}$.
又因为y1=lnx1-a(x1-1),消去y1和a后,整理得lnx1-1+$\frac{1}{{x}_{1}}$-$\frac{1}{e}$=0.
令m(x)=lnx-1+$\frac{1}{x}$-$\frac{1}{e}$=0,则m′(x)=$\frac{1}{x}$-$\frac{1}{{x}^{2}}$=$\frac{x-1}{{x}^{2}}$,
m(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
若x1∈(0,1),因为m($\frac{1}{e}$)=-2+e-$\frac{1}{e}$>0,m(1)=-$\frac{1}{e}$<0,
所以x1∈($\frac{1}{e}$,1),
而a=$\frac{1}{{x}_{1}}$-$\frac{1}{e}$在x1∈($\frac{1}{e}$,1)上单调递减,所以$\frac{e-1}{e}$<a<$\frac{{e}^{2}-1}{e}$.
若x1∈(1,+∞),因为m(x)在(1,+∞)上单调递增,且m(e)=0,则x1=e,
所以a=$\frac{1}{{x}_{1}}$-$\frac{1}{e}$=0(舍去).
综上可知,$\frac{e-1}{e}$<a<$\frac{{e}^{2}-1}{e}$.
故选:C.
点评 本题考查了利用导数求曲线的切线问题及单调性的运用,考查了化简整理的计算能力,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
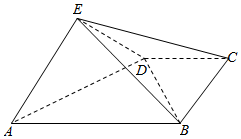 如图,四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2.
如图,四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在数列{an}中,a1=1,an=$\frac{1}{2}$(an-1+$\frac{1}{{a}_{n-1}}$)(n∈N*),由其归纳出{an}的通项公式 | |
| B. | 由平面三角形的性质,推测空间四面体性质 | |
| C. | 两条直线平行,同旁内角互补,如果∠A和∠B是两条平行直线的同旁内角,则∠A+∠B=180° | |
| D. | 某校高二共10个班,1班51人,2班53人,3班52人,由此推测各班都超过50人 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{BD}$ | B. | $\overrightarrow{AC}$ | C. | $\overrightarrow 0$ | D. | $\overrightarrow{AB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{5}{3}$ | C. | $\frac{{\sqrt{37}}}{3}$ | D. | $\frac{{\sqrt{35}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com