
分析 (1)通过求导可知函数G(x)=f(x)-g(x)的导函数表达式,进而解不等式即得结论;
(2)通过数学归纳法可证明0<an≤1,利用(1)可知对任意n∈N*恒有$ln({n+1})>\frac{n}{n+1}$,进而可得$\frac{1}{{{a_{n+1}}}}-\frac{1}{a_n}<1$,并项相加、放缩即得结论.
解答 (1)解:依题意可知:x>1,且${G^'}(x)=\frac{{x-({1+a})}}{{{{({x-1})}^2}}}$,
当a≤0时,G′(x)≥0,故G(x)在(1,+∞)上是增加的;
当a>0时,x∈(1,1+a)时,G′(x)≤0,此时G(x)是减少的,
当x∈(1+a,+∞)时,G′(x)≥0,此时G(x)是增加的;
(2)证明:依题意:an+1=ln(an+1),
先用数学归纳法证明0<an≤1,
①易知n=1时,0<an≤1成立,
②假设n=k(k∈N*)时,有0<ak≤1成立,
则0<ln(ak+1)≤ln2<1,则0<ak+1<1,
故n=k+1时,0<an≤1也成立,
综上知0<an≤1对任意n∈N*恒成立.
由(1)知当a=1时,$G(x)=f(x)-g(x)=ln({x-1})-\frac{x-2}{x-1}$在(2,+∞)上是增加的,
又∵G(2)=0,
∴对任意x≥2恒有$ln({x-1})≥\frac{x-2}{x-1}$,即任意n∈N*恒有$ln({n+1})>\frac{n}{n+1}$,
∵an+1=ln(an+1),$ln({{a_n}+1})>\frac{{{a_{{n_{\;}}}}}}{{{a_n}+1}}$,
∴$\frac{1}{{{a_{n+1}}}}<\frac{1}{a_n}+1$,即$\frac{1}{{{a_{n+1}}}}-\frac{1}{a_n}<1$,
故n>1时,有$\frac{1}{a_2}-\frac{1}{a_1}+\frac{1}{a_3}-\frac{1}{a_2}+…+\frac{1}{a_n}-\frac{1}{{{a_{n-1}}}}<n-1$,
所以$\frac{1}{a_n}<n$,即${a_n}>\frac{1}{n}$,
又∵当n=1时,an=1,
∴${a_n}≥\frac{1}{n}$,
故$\frac{1}{n}≤{a_n}≤1$成立.
点评 本题是一道关于数列与不等式的综合题,涉及利用导数研究函数的单调性、数学归纳法等基础知识,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -1 | C. | 1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
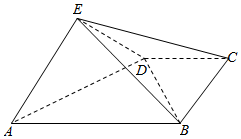 如图,四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2.
如图,四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在数列{an}中,a1=1,an=$\frac{1}{2}$(an-1+$\frac{1}{{a}_{n-1}}$)(n∈N*),由其归纳出{an}的通项公式 | |
| B. | 由平面三角形的性质,推测空间四面体性质 | |
| C. | 两条直线平行,同旁内角互补,如果∠A和∠B是两条平行直线的同旁内角,则∠A+∠B=180° | |
| D. | 某校高二共10个班,1班51人,2班53人,3班52人,由此推测各班都超过50人 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com