
分析 (Ⅰ)依题意,当n≥2时,由2an=2Sn-2Sn-1可得)an=1-n(n≥2),再检验n=1时,是否适合,以确定是分是合,从而可得数列{an}的通项公式;
(Ⅱ)由$\frac{2}{(1-{a}_{n})(1-{a}_{n+2})}=\frac{2}{n(n+2)}=\frac{1}{n}-\frac{1}{n+2}$可得T2n=(b1+b3+…+b2n-1)+(b2+b4+…+b2n),分组求和即可.
解答 解:(Ⅰ)当n≥2时,$2{a_n}=2{S_n}-2{S_{n-1}}=n-{n^2}-[(n-1)-{(n-1)^2}]=2-2n$--------(2分)
即:an=1-n(n≥2),-------------------------------------------------------------(3分)
当n=1时,由$2{S_1}=1-{1^2}$得a1=0,-----------------------------------------------(4分)
显然当n=1时上式也适合,
∴an=1-n.--------------------------------------------------------------------(5分)
(Ⅱ)∵$\frac{2}{{(1-{a_n})(1-{a_{n+2}})}}=\frac{2}{n(n+2)}=\frac{1}{n}-\frac{1}{n+2}$,------------------------------------(6分)
∴T2n=(b1+b3+…+b2n-1)+(b2+b4+…+b2n)-------------------------------------(7分)
=$({2^0}+{2^{-2}}+…+{2^{2-2n}})+[(\frac{1}{2}-\frac{1}{4})+(\frac{1}{4}-\frac{1}{6})+…+(\frac{1}{2n}-\frac{1}{2n+2})$]---------------------(9分)
=$\frac{{1-{{(\frac{1}{4})}^n}}}{{1-\frac{1}{4}}}+\frac{1}{2}-\frac{1}{2n+2}$---------------------------------------------------------(11分)
=$\frac{11}{6}-\frac{4}{3}•{(\frac{1}{4})^n}-\frac{1}{2n+2}$.-------------------------------------------------------(12分)
点评 本题考查数列的求和,着重考查数列递推式的应用,考查裂项法、公式法与分组求和法的综合应用,属于中档题.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{3}$ | B. | 2 | C. | $\frac{\sqrt{6}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{1}{4}$x | B. | y=±$\frac{1}{2}$x | C. | y=±4x | D. | y=±2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
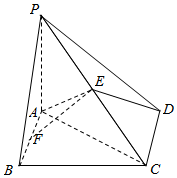 如图,在四棱锥中P-ABCD,底面ABCD为边长为$\sqrt{2}$的正方形,PA⊥BD.
如图,在四棱锥中P-ABCD,底面ABCD为边长为$\sqrt{2}$的正方形,PA⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,△ABE为等边三角形,且平面ABCD⊥平面ABE,CD=BC=$\frac{1}{2}$AB=1,点P为CE中点.
如图所示,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,△ABE为等边三角形,且平面ABCD⊥平面ABE,CD=BC=$\frac{1}{2}$AB=1,点P为CE中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
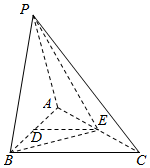 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
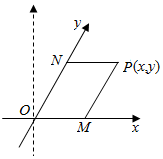 如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M,N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为x2+y2+xy-1=0.
如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M,N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为x2+y2+xy-1=0.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com