
分析 (1)由A={x|2≤x<4},B={x|3x-7≥8-2x}={x|x≥3},能求出A∩B.
(2)先由B和R,求出CRB,再求A∪(CUB).
(3)由集合A={x|2≤x<4},C={x|x<a},且A⊆C,能求出a的取值范围.
解答 解:(1)∵A={x|2≤x<4},
B={x|3x-7≥8-2x}
={x|x≥3},
∴A∩B={x|2≤x<4}∩{x|x≥3}
={x|3≤x<4}.
(2)∵CRB={x|x<3},
∴A∪(CUB)={x|2≤x<4}∪{x|x<3}
={x|x<4}.
(3)∵集合A={x|2≤x<4},C={x|x<a},
且A⊆C,
∴a≥4.
点评 本题考查集合的交、并、补集的混合运算,是基础题.解题时要认真审题,仔细解答.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:选择题
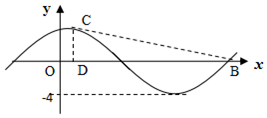 已知函数f(x)=Asin($\frac{1}{2}$x+φ),x∈R,(其中,|φ|<$\frac{π}{2}$)的部分图象如图所示,设点($\frac{2π}{3}$,4)是图象上y轴右侧的第一个最高点,CD⊥DB,D是y轴右侧第二个对称中心,则△DBC的面积是( )
已知函数f(x)=Asin($\frac{1}{2}$x+φ),x∈R,(其中,|φ|<$\frac{π}{2}$)的部分图象如图所示,设点($\frac{2π}{3}$,4)是图象上y轴右侧的第一个最高点,CD⊥DB,D是y轴右侧第二个对称中心,则△DBC的面积是( )| A. | 3 | B. | 4π | C. | 6π | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20π | B. | 24π | C. | 28π | D. | 32π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com