
| π |
| 2 |
| 4 |
| 5 |
科目:高中数学 来源: 题型:
| m |
| n |
| m |
| n |
| π |
| 2 |
| 14 |
| 5 |
| 31 |
| 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
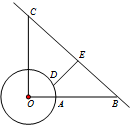 为了适应市场需要,某地准备建一个圆形生猪储备基地(如图),它的附近有一条公路,从基地中心O处向东走1km是储备基地的边界上的点A,接着向东再走7km到达公路上的点B;从基地中心O向正北走8km到达公路的另一点C.现准备在储备基地的边界上选一点D,修建一条由D通往公路BC的专用线DE,则DE的最短距离为
为了适应市场需要,某地准备建一个圆形生猪储备基地(如图),它的附近有一条公路,从基地中心O处向东走1km是储备基地的边界上的点A,接着向东再走7km到达公路上的点B;从基地中心O向正北走8km到达公路的另一点C.现准备在储备基地的边界上选一点D,修建一条由D通往公路BC的专用线DE,则DE的最短距离为查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4 |
| A |
| 1 |
| B+C |
| 9 |
| π |
| nπ |
| 6 |
| 16 | ||
2+sin
|
| 19 |
| 3 |
| f(a) |
| a |
| f(b) |
| b |
| f(c) |
| c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com