
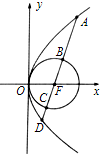 如图,抛物线y2=2px(p>0)和圆x2+y2-px=0,直线l经过抛物线的焦点,依次交抛物线与圆于A,B,C,D四点,|AB|•|CD|=2则p的值为( )
如图,抛物线y2=2px(p>0)和圆x2+y2-px=0,直线l经过抛物线的焦点,依次交抛物线与圆于A,B,C,D四点,|AB|•|CD|=2则p的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 求得抛物线的焦点和准线方程,圆的圆心和半径,设A(x1,y1),D(x2,y2),讨论若直线的斜率不存在,则直线方程为x=$\frac{p}{2}$,求出A,B,C,D的坐标,求得AB,CD的长,解方程可得p;若直线的斜率存在,设为k,则直线方程为y=k(x-$\frac{p}{2}$),代入抛物线的方程,运用韦达定理,结合抛物线的定义和圆的定义,可得p的方程,即可得到所求值.
解答 解:抛物线y2=2px焦点F($\frac{p}{2}$,0),准线方程为x=-$\frac{p}{2}$,
圆(x-$\frac{p}{2}$)2+y2=$\frac{1}{4}$p2的圆心是($\frac{p}{2}$,0)半径r=$\frac{p}{2}$,
设A(x1,y1),D(x2,y2),
过抛物线y2=4px的焦点F的直线依次交抛物线及圆(x-$\frac{p}{2}$)2+y2=$\frac{1}{4}$p2于点A,B,C,D,
A,D在抛物线上,B,C在圆上
①.若直线的斜率不存在,则直线方程为x=$\frac{p}{2}$,
代入抛物线方程和圆的方程,
可直接得到ABCD四个点的坐标为($\frac{p}{2}$,p),($\frac{p}{2}$,$\frac{p}{2}$),($\frac{p}{2}$,-$\frac{p}{2}$)($\frac{p}{2}$,-p),
所以|AB|•|CD|=$\frac{1}{2}$p•$\frac{1}{2}$p=2,
解得p=2$\sqrt{2}$;
②.若直线的斜率存在,设为k,则直线方程为y=k(x-$\frac{p}{2}$),
因为直线过抛物线的焦点($\frac{p}{2}$,0),
不妨设A(x1,y1),D(x2,y2),
由抛物线的定义,|AF|=x1+$\frac{p}{2}$,|DF|=x2+$\frac{p}{2}$,
把直线方程与抛物线方程联立,消去y可得
k2x2-(pk2+2p)x+$\frac{1}{4}$p2k2=0,
由韦达定理有x1x2=$\frac{1}{4}$p2,
而抛物线的焦点F同时是已知圆的圆心,
所以|BF|=|CF|=r=$\frac{1}{2}$p,
从而有|AB|=|AF|-|BF|=x1,
|CD|=|DF|-|CF|=x2,
由|AB|•|CD|=2,即有x1x2=2,
由$\frac{1}{4}$p2=2,解得p=2$\sqrt{2}$.
故选:D.
点评 本题主要考查抛物线标准方程,简单几何性质,直线与抛物线的位置关系,圆的简单性质等基础知识.考查运算求解能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>1} | B. | {x|x>0} | C. | {x|0<x<2} | D. | {x|1<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,0) | B. | [0,1] | C. | (0,1] | D. | [-2,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com