Question

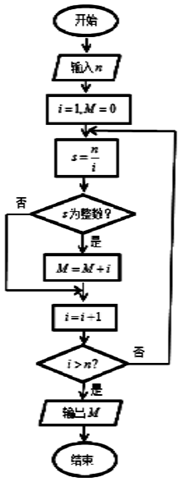
20．执行如图所示的程序框图，如果输入的n=32，那么输出的M=（　　）

• A． 66
• B． 65
• C． 64
• D． 63

Answer 1

分析 根据框图的流程模拟运行程序，直到满足条件，跳出循环，计算输出M的值，即可得解．

解答 解：模拟程序的运行，可得
当i=1，M=0，执行循环体，s=32，满足条件s为整数，M=1，
当i=2，不满足条件i＞32，执行循环体，s=16，满足条件s为整数，M=3，
当i=4，不满足条件i＞32，执行循环体，s=8，满足条件s为整数，M=3+4=7
当i=8，不满足条件i＞32，执行循环体，s=4，满足条件s为整数，M=7+8=15
当i=16，不满足条件i＞32，执行循环体，s=2，满足条件s为整数，M=15+16=31
当i=32，不满足条件i＞32，执行循环体，s=1，满足条件s为整数，M=31+32=63，
故选：D．

点评 本题考查了直到型循环结构的程序框图，根据框图的流程模拟运行程序是解答此类问题的常用方法，属于基础题．