
分析 由同角三角函数基本关系可得sinθ,代入两角和的正弦公式计算可得.
解答 解:∵cosθ=-$\frac{3}{5}$,θ∈($\frac{π}{2}$,π),
∴sinθ=$\sqrt{1-co{s}^{2}θ}$=$\frac{4}{5}$,
∴sin(θ+$\frac{π}{3}$)=sinθcos$\frac{π}{3}$+cosθsin$\frac{π}{3}$
=$\frac{4}{5}×\frac{1}{2}$+(-$\frac{3}{5}$)×$\frac{\sqrt{3}}{2}$=$\frac{4-3\sqrt{3}}{10}$
点评 本题考查两角和与差的正弦函数,涉及同角三角函数基本关系,属基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1-2\sqrt{6}}{6}$ | B. | -$\frac{1+2\sqrt{6}}{6}$ | C. | $\frac{1+2\sqrt{6}}{6}$ | D. | ±$\frac{1+2\sqrt{6}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2) | B. | (-1-$\sqrt{2}$,1+$\sqrt{2}$) | C. | (-1-$\sqrt{2}$,-$\sqrt{2}$)∪(-$\sqrt{2}$,1+$\sqrt{2}$) | D. | (-1-$\sqrt{2}$,-2)∪(2,1+$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
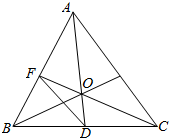 如图所示,已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,$\overrightarrow{OD}$=$\overrightarrow{d}$,$\overrightarrow{OF}$=$\overrightarrow{f}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,$\overrightarrow{f}$表示下列向量.
如图所示,已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,$\overrightarrow{OD}$=$\overrightarrow{d}$,$\overrightarrow{OF}$=$\overrightarrow{f}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,$\overrightarrow{f}$表示下列向量.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com