
| A. | [${\frac{4}{9}$,$\frac{5}{9}}$] | B. | [0,$\frac{3}{8}}$] | C. | [${\frac{3}{8}$,$\frac{4}{9}}$] | D. | [${\frac{5}{9}$,1) |
分析 由题意及椭圆的性质,可求得MF1=2a-2c,根据双曲线的性质求得A点的横坐标,求得$\frac{c}{a}$的取值范围,利用双曲线的离心率取值范围$\frac{3}{2}$≤$\frac{\frac{c}{a}}{1-\frac{2c}{a}}$≤4,椭圆离心率e1=$\frac{c}{a}$,
代入求得椭圆离心率e1的取值范围.
解答 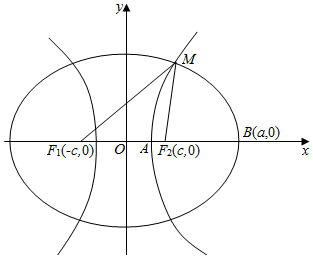 解:∵△MF1F2为等腰三角形,
解:∵△MF1F2为等腰三角形,
∴MF2=F1F2=2c,
根据椭圆定义应该有,MF2+MF1=2a=2c+MF1,可推出MF1=2a-2c,
∵双曲线也以F1和F2为焦点,根据其定义也有:MF1-MF2=(2a-2c)-2c=2a-4c,
∴A点横坐标为a-2c,由a-2c>0,得:0<$\frac{c}{a}$<$\frac{1}{2}$;
双曲线离心率e范围:$\frac{3}{2}$≤e=$\frac{丨O{F}_{2}丨}{丨OA丨}$=$\frac{c}{a-2c}$=$\frac{\frac{c}{a}}{1-\frac{2c}{a}}$≤4,①
因此求得椭圆离心率e1=$\frac{c}{a}$,
当0<e1<$\frac{1}{2}$时,解得①:$\frac{3}{8}$≤e1=$\frac{c}{a}$≤$\frac{4}{9}$;
故答案选:C.
点评 本题考查椭圆的离心率的取值范围的求法,解题时要认真审题,注意双曲线、椭圆性质的灵活运用,是中档题.


科目:高中数学 来源: 题型:解答题
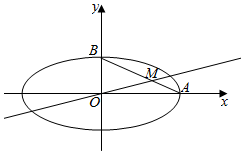 如图,椭圆E的方程为$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),点O为坐标原点,点A,B分别是椭圆的右顶点和上顶点,点M在线段AB上,满足BM=2MA,直线OM的斜率为$\frac{1}{4}$.
如图,椭圆E的方程为$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),点O为坐标原点,点A,B分别是椭圆的右顶点和上顶点,点M在线段AB上,满足BM=2MA,直线OM的斜率为$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 家庭月收入 (单位:元) | 2千以下 | 2千~5千 | 5千~8千 | 8千~一万 | 1万~2万 | 2万以上 |
| 调查的总人数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 有二孩计划的家庭数 | 1 | 2 | 9 | 7 | 3 | 4 |
| 收入不高于8千的家庭数 | 收入高于8千的家庭数 | 合计 | |
| 有二孩计划的家庭数 | |||
| 无二孩计划的家庭数 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)关于x=$\frac{5}{9}$π对称 | |
| B. | 函数f(x)向左平移$\frac{π}{18}$个单位后是奇函数 | |
| C. | 函数f(x)关于点($\frac{π}{18}$,0)中心对称 | |
| D. | 函数f(x)在区间[0,$\frac{π}{20}$]上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com