
分析 (1)利用平方和公式化简求解即可.
(2)利用对数运算法则化简求解即可.
解答 解:(1)$\frac{{m+{m^{-1}}+2}}{{{m^{-\frac{1}{2}}}+{m^{\frac{1}{2}}}}}=\frac{{{{({{m^{-\frac{1}{2}}}+{m^{\frac{1}{2}}}})}^2}}}{{{m^{-\frac{1}{2}}}+{m^{\frac{1}{2}}}}}={m^{-\frac{1}{2}}}+{m^{\frac{1}{2}}}$-----------------(5分)
(2)$\frac{lg8+lg125-lg2-lg5}{lg\sqrt{10}lg0.1}$=-----------------------------(2分)
=$\frac{{3({lg2+lg5})-(lg2+lg5)}}{{\frac{1}{2}lg10•lg{{10}^{-1}}}}=\frac{2}{{-\frac{1}{2}}}=-4$---------------------------(5分)
点评 本题考查有理指数幂以及对数运算法则的化简求解,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
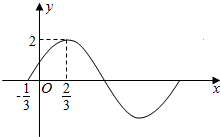 己知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)部分图象如图所示.
己知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)部分图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com