
| A. | 2$\sqrt{2}$ | B. | 5 | C. | 3 | D. | $\sqrt{10}$ |
分析 设$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角是θ且θ∈[0,π],由向量的书记运算求出$\overrightarrow{OA}$•$\overrightarrow{OB}$,对已知的式子两边同时平方后,由数量积运算化简后可求cosθ,由二倍角的余弦公式和θ的范围求出$cos\frac{θ}{2}$,由点到直线的距离公式求出圆心O到直线的距离,由三角函数列出方程求出r的值.
解答 解:由题意可得,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|=r,
设$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角是θ,且θ∈[0,π],
则$\overrightarrow{OA}$•$\overrightarrow{OB}$=|$\overrightarrow{OA}$||$\overrightarrow{OB}$|cosθ=r2cosθ,
由题意知,$\overrightarrow{OC}=\frac{5}{4}\overrightarrow{OA}+\frac{3}{4}\overrightarrow{OB}$,
则${\overrightarrow{OC}}^{2}=\frac{25}{16}{\overrightarrow{OA}}^{2}+\frac{15}{8}\overrightarrow{OA}•\overrightarrow{OB}+\frac{9}{16}{\overrightarrow{OB}}^{2}$,
所以${r}^{2}=\frac{25}{16}{r}^{2}+\frac{15}{8}{r}^{2}cosθ+\frac{9}{16}{r}^{2}$,
化简cosθ=$-\frac{3}{5}$,
因为cosθ=2$co{s}^{2}\frac{θ}{2}$-1,且$cos\frac{θ}{2}$>0,所以$-\frac{3}{5}$=2$co{s}^{2}\frac{θ}{2}$-1,
解得$cos\frac{θ}{2}$=$\frac{\sqrt{5}}{5}$,
设圆心O(0,0)到直线x+y-2=0的距离为d,
则d=$\frac{|-2|}{\sqrt{2}}$=$\sqrt{2}$,即r$cos\frac{θ}{2}$=$\sqrt{2}$,解得r=$\sqrt{10}$,
故选:D.
点评 本题考查了直线与圆的位置关系,点到直线的距离公式,二倍角的余弦公式,以及向量的数量积运算的灵活应用,考查了转化思想,化简、变形能力.


科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
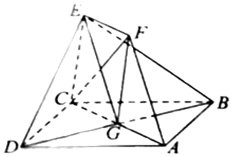 (理)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.
(理)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com