
已知在四棱锥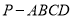 中,底面
中,底面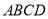 是矩形,且
是矩形,且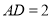 ,
, ,
, 平面
平面 ,
,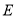 、
、 分别是线段
分别是线段 、
、 的中点.
的中点.
(1)证明:
(2)在线段 上是否存在点
上是否存在点 ,使得
,使得 ∥平面
∥平面 ,若存在,确定点
,若存在,确定点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
(3)若 与平面
与平面 所成的角为
所成的角为 ,求二面角
,求二面角 的余弦值
的余弦值

(1)证明见解析;(2)证明见解析;(3)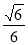
【解析】
试题分析:(1)利用已知的线面垂直关系建立空间直角坐标系,准确写出相关点的坐标,从而将几何证明转化为向量运算.其中灵活建系是解题的关键.(2)证明证线线垂直,只需要证明直线的方向向量垂直;(3)把向量夹角的余弦值转化为两平面法向量夹角的余弦值;(4)空间向量将空间位置关系转化为向量运算,应用的核心是要充分认识形体特征,建立恰当的坐标系,实施几何问题代数化.同时注意两点:一是正确写出点、向量的坐标,准确运算;二是空间位置关系中判定定理与性质定理条件要完备.
试题解析:解法一:(1)∵ 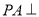 平面
平面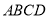 ,
, ,
, ,
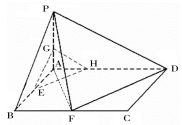
,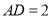 ,建立如图所示的空间直角坐标系
,建立如图所示的空间直角坐标系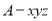 ,则
,则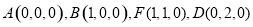 . 2分
. 2分
不妨令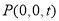 ∵
∵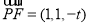 ,
, ∴
∴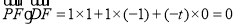 ,
,
即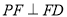 . 4分
. 4分

(2)设平面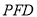 的法向量为
的法向量为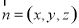 ,由
,由 ,得
,得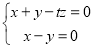 ,令
,令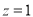 ,
,
得: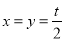 .∴
.∴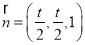 . 6分
. 6分
设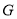 点坐标为
点坐标为
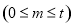 ,
, ,则
,则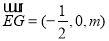 ,要使
,要使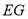 ∥平面
∥平面 ,只需
,只需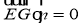 ,即
,即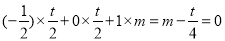 ,得
,得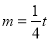 ,从而满足
,从而满足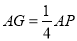 的点
的点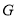 即为所求. 8分
即为所求. 8分
(3)∵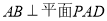 ,∴
,∴ 是平面
是平面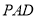 的法向量,易得
的法向量,易得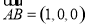 , 9分
, 9分
又∵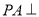 平面
平面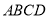 ,∴
,∴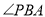 是
是 与平面
与平面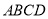 所成的角,
所成的角,
得 ,
,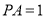 ,平面
,平面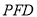 的法向量为
的法向量为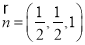 10分
10分
∴ ,
,
故所求二面角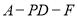 的余弦值为
的余弦值为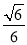 . 12分
. 12分
解法二:(1)证明:连接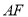 ,则
,则 ,
,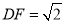 ,
,
又 ,∴
,∴  ,∴
,∴ 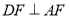 2分
2分
又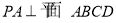 ,∴
,∴ 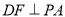 ,又
,又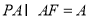 ,
,
∴ 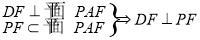 4分
4分
(2)过点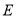 作
作 交
交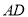 于点
于点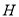 ,则
,则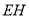 ∥平面
∥平面 ,且有
,且有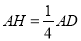 5分
5分
再过点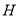 作
作 ∥
∥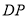 交
交 于点
于点 ,则
,则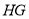 ∥平面
∥平面 且
且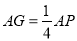 ,∴ 平面
,∴ 平面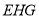 ∥平面
∥平面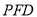 7分 ∴
7分 ∴  ∥平面
∥平面 .从而满足
.从而满足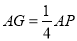 的点
的点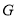 即为所求. 8分
即为所求. 8分
(3)∵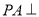 平面
平面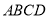 ,∴
,∴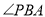 是
是 与平面
与平面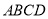 所成的角,且
所成的角,且 .
.
∴ 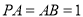 9分
9分
取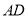 的中点
的中点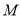 ,则
,则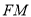

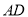 ,
,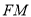
 平面
平面 ,
,
在平面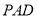 中,过
中,过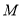 作
作 ,连接
,连接 ,则
,则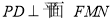 ,
,
则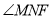 即为二面角
即为二面角 的平面角 10分
的平面角 10分
∵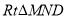 ∽
∽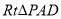 ,∴
,∴  ,∵
,∵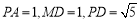 ,且
,且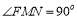
∴ 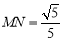 ,
,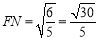 ,∴
,∴ 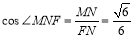 12分
12分
考点:1、直线与直线垂直的判定;2、直线与平面垂直的判定;3、二面角的余弦值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013-2014学年福建省龙岩市高三上学期期末考试理科数学试卷(解析版) 题型:填空题
定义在R上的函数f(x),满足f(m+n2)=f(m)+2[f(n)]2,m,n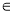 R,且f(1):≠0,则f(2014)的值为____
R,且f(1):≠0,则f(2014)的值为____
查看答案和解析>>
科目:高中数学 来源:2015届内蒙古巴彦淖尔市高三10月月考理科数学试卷(解析版) 题型:选择题
已知命题 ,使
,使 命题
命题 ,都有
,都有 给出下列结论:
给出下列结论:
①命题“ ”是真命题
”是真命题
②命题“ ”是假命题
”是假命题
③命题“ ”是真命题
”是真命题
④命题“ ”是假命题
”是假命题
其中正确的是( )
A.①②③ B.③④ C.②④ D.②③
查看答案和解析>>
科目:高中数学 来源:2015届内蒙古巴彦淖尔市高三10月月考文科数学试卷(解析版) 题型:选择题
设函数 ,则函数
,则函数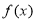 是( )
是( )
A.最小正周期为 的奇函数
的奇函数
B.最小正周期为 的奇函数
的奇函数
C.最小正周期为 的偶函数
的偶函数
D.最小正周期为 的偶函数
的偶函数
查看答案和解析>>
科目:高中数学 来源:2015届云南省等校高三12月份统一考试文科数学试卷(解析版) 题型:选择题
阅读如图的程序框图,运行相应的程序,若输入x的值为﹣4,则输出y的值为( )

A.0.5 B.1 C.2 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com