
【题目】已知函数![]() 在
在![]() 处取得极值A,函数
处取得极值A,函数![]() ,其中
,其中![]() …是自然对数的底数.
…是自然对数的底数.
(1)求m的值,并判断A是![]() 的最大值还是最小值;
的最大值还是最小值;
(2)求![]() 的单调区间;
的单调区间;
(3)证明:对于任意正整数n,不等式![]() 成立.
成立.
【答案】(1)![]() ;
;![]() 是最小值;(2)单调递减区间是
是最小值;(2)单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;(3)证明过程见详解.
;(3)证明过程见详解.
【解析】
(1)先对函数求导,根据题意,得到![]() ,求出
,求出![]() ,研究函数单调性,即可判断出结果;
,研究函数单调性,即可判断出结果;
(2)对函数![]() 求导,得到
求导,得到![]() ,令
,令![]() ,对其求导,研究其单调性,即可判断函数
,对其求导,研究其单调性,即可判断函数![]() 的单调性;
的单调性;
(3)先由(1)得![]() 时,
时,![]() 恒成立,令
恒成立,令![]() ,则
,则![]() ,进而求和,即可得出结果.
,进而求和,即可得出结果.
(1)因为![]() ,
,![]() ,所以
,所以![]() ,
,
又![]() 在
在![]() 处取得极值
处取得极值![]() ,
,
则![]() ,即
,即![]() ;所以
;所以![]() ,
,
由![]() 得
得![]() ;由
;由![]() 得
得![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
因此![]() 在
在![]() 处取得最小值,即
处取得最小值,即![]() 是最小值;
是最小值;
(2)由(1)得![]() ,
,
所以![]() ,
,
令![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() 恒成立,
恒成立,
因此![]() 在
在![]() 上单调递增;又
上单调递增;又![]() ,
,
所以,当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ;
;
所以函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;
;
(3)由(1)知,![]() ,
,
所以![]() ,当
,当![]() 时,
时,![]() 恒成立;
恒成立;
令![]() ,则
,则![]() ,
,
因此![]()
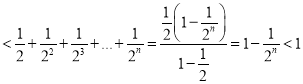 ,
,
即![]() ,
,
因此![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
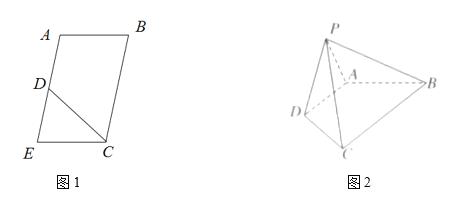
,![]() 是EA的中点(如图1),将
是EA的中点(如图1),将![]() 沿CD折起到图2中
沿CD折起到图2中![]() 的位置,得到四棱锥是
的位置,得到四棱锥是![]() .
.
(1)求证:![]() 平面PDA;
平面PDA;
(2)若PD与平面ABCD所成的角为![]() .且
.且![]() 为锐角三角形,求平面PAD和平面PBC所成锐二面角的余弦值.
为锐角三角形,求平面PAD和平面PBC所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由团中央学校部、全国学联秘书处、中国青年报社共同举办的2018年度全国“最美中学生”寻访活动结果出炉啦,此项活动于2018年6月启动,面向全国中学在校学生,通过投票方式寻访一批在热爱祖国、勤奋学习、热心助人、见义勇为等方面表现突出、自觉树立和践行社会主义核心价值观的“最美中学生”.现随机抽取了30名学生的票数,绘成如图所示的茎叶图,若规定票数在65票以上(包括65票)定义为风华组.票数在65票以下(不包括65票)的学生定义为青春组.
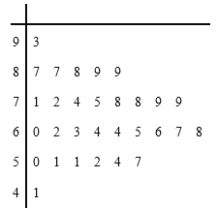
(1)如果用分层抽样的方法从青春组和风华组中抽取5人,再从这5人中随机抽取2人,那么至少有1人在青春组的概率是多少?
(2)用样本估计总体,把频率作为概率,若从该地区所有的中学(人数很多)中随机选取4人,用![]() 表示所选4人中青春组的人数,试写出
表示所选4人中青春组的人数,试写出![]() 的分布列,并求出
的分布列,并求出![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 上点
上点![]() 作三条斜率分别为
作三条斜率分别为![]() ,
,![]() ,
,![]() 的直线
的直线![]() ,
,![]() ,
,![]() ,与抛物线分别交于不同于
,与抛物线分别交于不同于![]() 的点
的点![]() .若
.若![]() ,
,![]() ,则以下结论正确的是( )
,则以下结论正确的是( )
A.直线![]() 过定点B.直线
过定点B.直线![]() 斜率一定
斜率一定
C.直线![]() 斜率一定D.直线
斜率一定D.直线![]() 斜率一定
斜率一定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车品牌为了了解客户对于其旗下的五种型号汽车的满意情况,随机抽取了一些客户进行回访,调查结果如下表:
汽车型号 | I | II | III | IV | V |
回访客户(人数) | 250 | 100 | 200 | 700 | 350 |
满意率 | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
满意率是指:某种型号汽车的回访客户中,满意人数与总人数的比值.
假设客户是否满意互相独立,且每种型号汽车客户对于此型号汽车满意的概率与表格中该型号汽车的满意率相等.
(1)从所有的回访客户中随机抽取1人,求这个客户满意的概率;
(2)从I型号和V型号汽车的所有客户中各随机抽取1人,设其中满意的人数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)用 “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”分别表示I, II, III, IV, V型号汽车让客户满意, “
”分别表示I, II, III, IV, V型号汽车让客户满意, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ” 分别表示I, II, III, IV, V型号汽车让客户不满意.写出方差
” 分别表示I, II, III, IV, V型号汽车让客户不满意.写出方差![]() 的大小关系.
的大小关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com