
分析 先求出数列的前几项,然后总结归纳其中的规律,写出其通项.
解答 解:由已知中单项式:-x,2x2,-3x3,4x4,…,-19x19,20x20,…
归纳可得:
(1)奇数项系数为-,偶数项系数为+,
系数的绝对值及次数均等于项数;
(2)第100个单项式为100x100,第2015个单项式为-2015x2015;
(3)写出第n个单项式为(-1)nnxn,第(n+1)个单项式为(-1)n+1(n+1)xn+1.
点评 本题考查的知识点是归纳推理,方法是根据已知条件和递推关系,归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
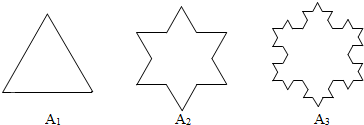
| A. | 16 | B. | $\frac{16}{3}$ | C. | $\frac{256}{9}$ | D. | $\frac{128}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
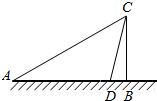 如图,某人欲测量某建筑物的高度BC,在A处测得建筑物顶端C的仰角为30°,然后,向建筑物方向前进200m到达D处,在D处测得C的仰角为75°,则建筑物的高度为( )
如图,某人欲测量某建筑物的高度BC,在A处测得建筑物顶端C的仰角为30°,然后,向建筑物方向前进200m到达D处,在D处测得C的仰角为75°,则建筑物的高度为( )| A. | 50($\sqrt{3}$+1)m | B. | 50($\sqrt{2}$+1)m | C. | 50($\sqrt{3}$-1)m | D. | 50($\sqrt{3}$+$\sqrt{2}$) m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com